mixedmath

It is that time of year. Classes are over. Campus is emptying. Soon it will be mostly emptiness, snow, and grad students (who of course never leave).

I like to take some time to reflect on the course. How did it go? What went well and what didn't work out? And now that all the numbers are in, we can examine course trends and data.

Since numbers are direct and graphs are pretty, let's look at the numbers first.

Math 100 grades at a glance

Let's get an understanding of the distribution of grades in the course, all at once.

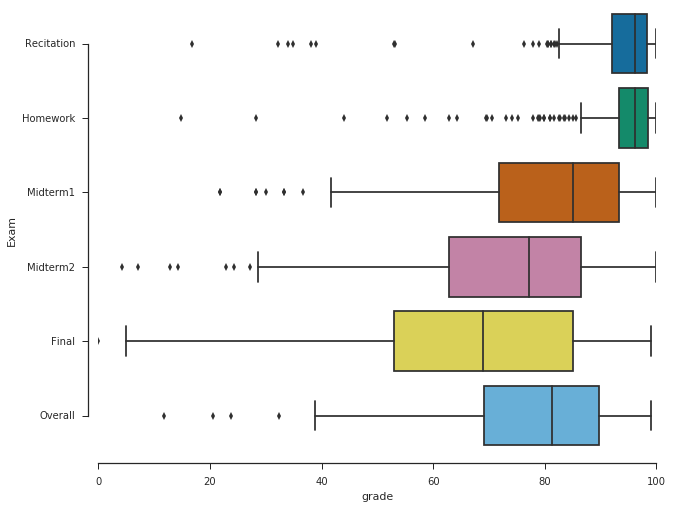
These are classic box plots. The center line of each box denotes the median. The left and right ends of the box indicate the 1st and 3rd quartiles. As a quick reminder, the 1st quartile is the point where 25% of students received that grade or lower. The 3rd quartile is the point where 75% of students received that grade or lower. So within each box lies 50% of the course.

Each box has two arms (or "whiskers") extending out, indicating the other grades of students. Points that are plotted separately are statistical outliers, which means that they are $1.5 \cdot (Q_3 - Q_1)$ higher than $Q_3$ or lower than $Q_1$ (where $Q_1$ denotes the first quartile and $Q_3$ indicates the third quartile).

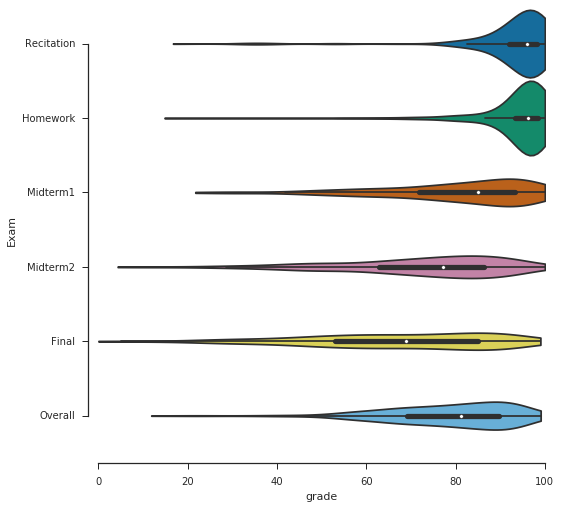
A bit more information about the distribution itself can be seen in the following graph.

Within each blob, you'll notice an embedded box-and-whisker graph. The white dots indicate the medians, and the thicker black parts indicate the central 50% of the grade. The width of the colored blobs roughly indicate how many students scored within that region. [As an aside, each blob actually has the same area, so the area is a meaningful data point].

So what can we determine from these graphs? Firstly, students did extremely well in their recitation sections and on the homework. I am perhaps most stunned by the tightness of the homework distribution. Remarkably, 75% of students had at least a 93 homework average. Recitation scores were very similar.

I also notice some patterns between the two midterms and final. The median on the first midterm was very high and about 50% of students earned a score within about 12 points of the median. The median on the second midterm was a bit lower, but the spread of the middle 50% of students was about the same. However the lower end was significantly lower on the second midterm in comparison to the first midterm. The median on the final was significantly lower, and the 50% spread was much, much larger.

Looking at the Overall grade, it looks very similar to the distribution of the first midterm, except shifted a bit.

It is interesting to note that that Recitation (10%), Homework (20%), and the First Midterm (20%) accounted for 50% of the course grade; the Second Midterm (20%) and the Final (30%) accounted for the other 50% of the course grade. The Recitation, Homework, and First Midterm grades pulled the Overall grade distribution up, while the Second Midterm and Final pulled the Overall grade distribution down.

Correlation between assignments and Overall Grade

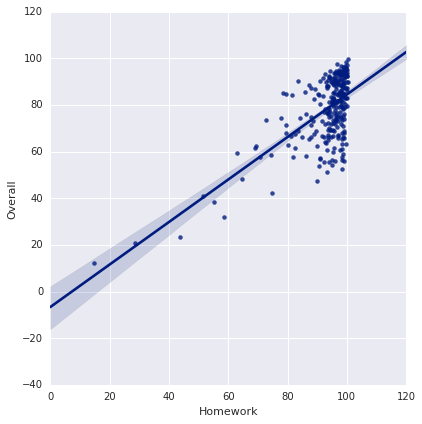
I post the question: was any individual assignment type a good predictor of the final grade? For example, to what extent can we predict your final grade based on your First Midterm grade?

No, doing well on homework is a terrible predictor of final grade. The huge vertical cluster of dots indicates that the overall grades vary significantly over a very small amount of homework. However, I note that doing poorly on homework is a great predictor of doing poorly overall. No one whose homework average was below an 80 got an A in the course. Having a homework grade below a 70 is a very strong indicator of failing the course. In terms of Pearson's R correlation, one might say that about 40% of overall performance is predicted from performance on homework (which is very little).

Although drastic, this is in line with my expectations for calculus courses. This is perhaps a bit more extreme than normal — the level of clustering in the homework averages is truly stunning. Explaining this is a bit hard. It is possible to get homework help from the instructor or TA, or to work with other students, or to get help from the Math Resource Center or other tutoring. It is also possible to cheat, either with a solutions manual (which I know some students have), or a paid answer service (which I also witnessed), or to check answers on a computer algebra system like WolframAlpha. Each of these weakens the relationship between homework as an indicator of mastery.

In the calculus curriculum at Brown, I think it's safe to say that homework plays a formative role instead of a normative role. It serves to provide opportunities for students to work through and learn material, and we don't expect the grades to correspond strongly to understanding. To that end, half of the homework isn't even collected.

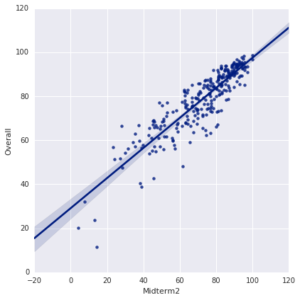
The two midterms each correlate pretty strongly with Overall grade. In particular, the second midterm visually indicates really strong correlation. Statistically speaking (i.e. from Pearson's R), it turns out that 67% of the Overall grade can be predict from the First Midterm (higher than might be expected) and 80% can be predicted from the Second Midterm (which is really, really high).

If we are willing to combine some pieces of information, the Homework and First Midterm (together) predict 77% of the Overall grade. As each student's initial homework effort is very indicative of later homework, this means that we can often predict a student's final grade (to a pretty good accuracy) as early as the first midterm.

(The Homework and the Second Midterm together predict 85% of the Overall grade. The two midterms together predict 88% of the Overall grade.)

This has always surprised me a bit, since for many students the first midterm is at least partially a review of material taught before. However, this course is very cumulative, so it does make sense that doing poorly on earlier tests indicates a hurdle that must be overcome in order to succeed on later tests. This is one of the unforgiving aspects of math, the sciences, and programming — early disadvantages compound. I've noted roughly this pattern in the past as well.

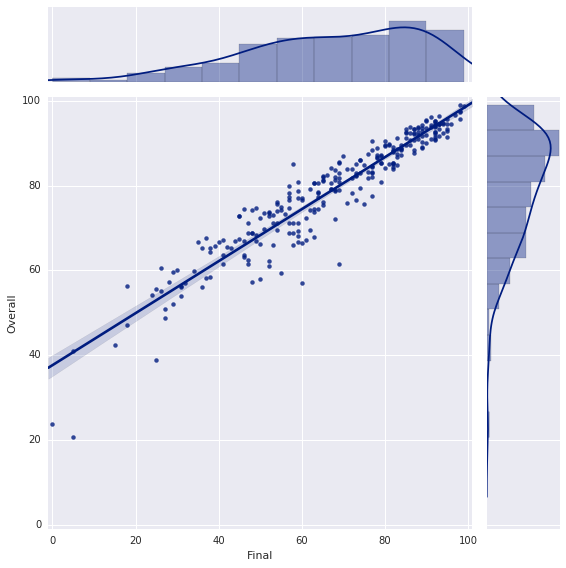
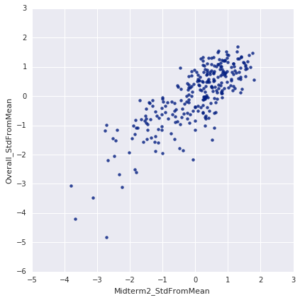
However the correlation between the Final and the Overall grade is astounding. I mean, look at how much the relationship looks like a line. Even the distributions (shown around the edges) look similar. Approximately 90% of the Overall grade is predicted by the grade on the Final Exam.

This is a bit atypical. One should expect a somewhat high correlation, as the final exam is cumulative and covers everything from the course (or at least tries to). But 90% is extremely high.

I think one reason why this occurred this semester is that the final exam was quite hard. It was distinctly harder than the midterms (though still easier than many of the homework problems). A hard final gives more opportunities for students who really understand the material to demonstrate their mastery. Conversely, a hard final punishes students with only a cursory understanding. Although stressful, I've always been a fan of exams that are difficult enough to distinguish between students, and to provide a chance for students to catch up. See Chances for a Comeback below for more on this.

Related statistics of interest might concern to what extent performance on the First Midterm predicts performance on the Second Midterm (44%) or the Final Exam (48%), or to what extent the Second Midterm predicts performance on the Final Exam (63%).

Homework and Recitations

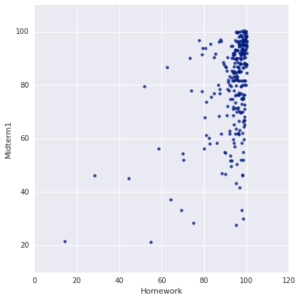As mentioned above, homework performance is a terrible predictor of course grade. I thought it was worth diving into a bit more. Does homework performance predict anything well? The short answer is not really.

Plotting Homework grade vs the First Midterm shows such a lack of meaning that it doesn't even make sense to try to draw a line of best fit.

To be fair, homework is a better predictor of performance on the Second Midterm and Final Exam, but it's still very bad.

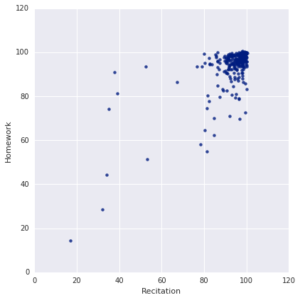Here's a related question: what about Recitation sections? Are these good predictors of any other aspect of the course?

Plotting Recitation vs Homework is sort of interesting. Evidently, most people did very well on both homework and recitation. It is perhaps no surprise that most students who did very well in Recitation also did very well on their Homework, and vice versa. However it turns out that there are more people with high recitation grades and low homework grades than the other way around. But thinking about it, this makes sense.

These distributions are so tight that it still doesn't make sense to try to draw a line of best fit or to talk about Pearson coefficients - most variation is simply too small to be meaningful.

Together, Homework and Recitation predict a measly 50% of the Overall grade of the course (in the Pearson's R sense). One would expect more, as Homework and Recitation are directly responsible for 30% of the Overall grade, and one would expect homework and recitation to correlate at least somewhat meaningfully with the rest of graded content of the course, right?

I guess not.

So what does this mean about recitation and homework? Should we toss them aside? Does something need to be changed?

I would say "Not necessarily," as it is important to recognize that not all grades are equal. Both homework and recitation are the places for students to experiment and learn. Recitations are supposed to be times where students are still learning material. They are to be inoffensive and safe, where students can mess up, fall over, and get back up again with the help of their peers and TA. I defend the lack of stress on grade or challenging and rigorous examination during recitation.

Homework is sort of the same, and sort of completely different. What gives me pause concerning homework is that homework is supposed to be the barometer by which students can measure their own understanding. When students ask us about how they should prepare for exams, our usual response is "If you can do all the homework (including self-check) without referencing the book, then you will be well-prepared for the exam." If homework grade is such a poor predictor of exam grades, then is it possible that homework gives a poor ruler for students to measure themselves by?

I'm not sure. Perhaps it would be a good idea to indicate all the relevant questions in the textbook so that students have more problems to work on. In theory, students could do this themselves (and for that matter, I'm confident that such students would do very well in the course). But the problem is that we only cover a subset of the material in most sections of the textbook, and many questions (even those right next to ones we assign) require ideas or concepts that we don't teach.

On the other hand, learning how to actually learn is a necessary skill, and probably one that most people struggle with when they first actually have to learn it. It's necessary to learn it sooner or later.

Chances for a Comeback

The last numerical aspect I'll consider is about whether or not it is possible to come back after doing badly on an earlier assessment. There are two things to consider: whether it is actually feasible or not, and whether any students did make it after a poor initial/early performance.

As to whether it is possible, the answer is yes (but it may be hard). And the reason why is that the Second Midterm and Final grades were each relatively low. It may be counterintuitive, but in order to return from a failing grade, it is necessary that there be enough room to actually come back.

Suppose Aiko is a pretty good student, but it just so happens that she makes a 49 on the first midterm due to some particular misunderstanding. If the class average on every assessment is a 90, then Aiko cannot claw her way back. That is, even if Aiko makes a 100 on everything else, Aiko's final grade would be below a 90, and thus below average. Aiko would probably make a B.

In this situation, the class is too easy, and thus there are no chances for students to overcome a setback on any single exam.

On the other hand, suppose that Bilal makes a 49 on the first midterm, but that the class average is a 75 overall. If Bilal makes a 100 on everything else, Bilal will  end with just below a 90, significantly above the class average. Bilal would probably make an A.

In this course, the mean overall was a 78, and the standard deviation was about 15. In this case, an 89 would be an A. So there was enough space and distance to overcome even a disastrous exam.

But, did anyone actually do this? The way I like to look at this is to look at changes in relative performance in terms of standard deviations away from the mean. Performing at one standard deviation below the mean on Midterm 1 and one standard deviation above the mean on Midterm 2 indicates a more meaningful amount of grade fluidity than merely looking at points above or below the mean

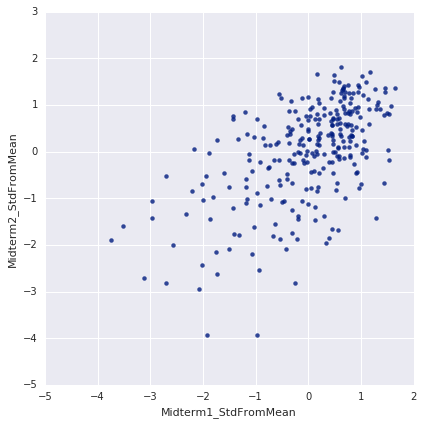
Looking at the First Midterm vs the Second Midterm, we see that there is a rough linear relationship (Pearson R suggests 44% predictive value). That's to be expected. What's relevant now are the points above or below the line $y = x$. To be above the line $y = x$ means that you did better on the Second Midterm than you did on the First Midterm, all in comparison to the rest of the class. To be below means the opposite.

Even more relevant is to be in the Fourth Quadrant, which indicates that you did worse than average on the first midterm and better than average on the second. Looking here, there is a very healthy amount of people who are in the Fourth Quadrant. There are many people who changed by 2 standard deviations in comparison to the mean — a very meaningful change. [Many people lost a few standard deviations too - grade mobility is a two way street].

The First Midterm to the Overall grade shows healthy mobility as well.

The Second Midterm to Overall shows some mobility, but it is interesting that more people lost ground (by performing well on the Second Midterm, and then performing badly Overall) than gained ground (by performing badly on the Second Midterm, but performing well Overall).

Although I don't show the plots, this trend carries through pretty well. Many people were able to salvage or boost a letter grade based solely on the final (and correspondingly many people managed to lose just enough on the final to drop a letter grade). Interestingly, very many people were able to turn a likely B into an A through the final.

So overall, I would say that it was definitely possible to salvage grades this semester.

If you've never thought about this before, then keep this in mind the next time you hear complaints about a course with challenging exams — it gives enough space for students to demonstrate sufficient understanding to make up for a bad past assessment.

Non-Numerical Reflection

The numbers tell some characteristics of the class, but not the whole story.

Standard Class Materials

We used Thomas' Calculus. I think this is an easy book to teach from, and relatively easy to read. It feels like many other cookie-cutter calculus books (such as Larson and Edwards or Stewart). But it's quite expensive for students. However, as we do not use an electronic homework component (which seems to be becoming more popular elsewhere), at least students can buy used copies (or use other methods of procural).

However, solutions manuals are available online (I noticed some students had copies). Some of the pay-for sites have complete (and mostly but not entirely correct) provided solutions manuals as well. This makes some parts of Thomas challenging to use, especially as we do not write our own homework to give. I suppose that this is a big reason why one might want to use an electronic system.

The book has much more material in it than we teach. For instance, the book includes all of a first semester of calculus, and also more details in many sections. We avoid numerical integration, Fourier series, some applications, some details concerning polar and parametric plots, etc. Ideally, there would exist a book catering to exactly our needs. But there isn't, so I suppose Thomas is about as good as any.

Additional Course Materials

I've now taught elementary calculus for a few years, and I'm surprised at how often I am able to reuse two notes I wrote years ago, namely the refresher on first semester calculus (An Intuitive Introduction to Calculus) and my additional note on Taylor series (An Intuitive Overview of Taylor Series). Perhaps more surprisingly, I'm astounded at how often people from other places link to and visit these two notes (and in particular, the Taylor Series note).

These were each written for a Math 100 course in 2013. So my note to myself is that there is good value in writing something well enough that I can reuse it, and others might even find it valuable.

Unfortunately, while I wrote a few notes this semester, I don't think that they will have the same lasting appeal. The one I wrote on the series convergence tests is something that (perhaps after one more round of editing) I will use each time I teach this subject in the future. I'm tremendously happy with my note on computing $\pi$ with Math 100 tools, but as it sits outside the curriculum, many students won't actually read it. [However many did read it, and it generated many interesting conversations about actual mathematics]. Perhaps sometime I will teach a calculus class ending with some sort of project, as computing $\pi$ leads to very many interested and interrelated project thoughts.

Course Content

I must admit that I do not know why this course is the way it is, and this bothers me a bit. In many ways, this course is a grab bag of calculus nuggets. Presumably each piece was added in because it is necessary in sufficiently many other places, or is so directly related to the "core material" of this course, that it makes sense to include it. But from what I can tell, these reasons have been lost to the sands of time.

The core material in this course are: Integration by Parts, Taylor's Theorem, Parametric and Polar coordinates, and First Order Linear Differential Equations. We also spend a large amount of time towards other techniques of integration (partial fraction decomposition, trig substitution) and understanding generic series (including the various series convergence/divergence tests). Along the way, there are some seemingly arbitrary decisions on what to include or exclude. For instance, we learn how to integrate

$$ \int \sin^n x \cos^m x \; dx$$

because we have decided that being able to perform trigonometric substitution in integrals is a good idea. But we omit integrals like

$$ \int \sin(nx) \sin(mx) \; dx$$

which would come up naturally in talking about Fourier series. Fourier series fit naturally into this class, and in some variants of this class they are taught. But so does trigonometric substitution! So what is the rationale here? If the answer is to become better at problem solving or to develop mathematical maturity, then I think it would be good to recognize that so that we know what we should feel comfortable wiggling to build and develop the curriculum in the future. [Also, students should know that calculus is not a pinnacle. See for instance this podcast with Steven Strogatz on Innovation Hub.]

This is not restricted to Brown. I'm familiar with the equivalent of this course at other institutions, and there are similar seemingly arbitrary differences in what to include or exclude. For years at Georgia Tech, they tossed in a several week unit on linear algebra into this course [although I've learned that they stopped that in the past two years]. The AP Calc BC curriculum includes trig substitution but not Fourier series. Perhaps they had a reason?

What this means to me is that the intent of this course has become muddled, and separated from the content of the course. This is an overwhelmingly hard task to try to fix, as a second semester of calculus fits right in the middle of so many other pieces. Yet I would be very grateful to the instructor who sits down and identifies reasons for or against inclusion of the various topics in this course, or perhaps cuts the calculus curriculum into pieces and rearranges them to fit modern necessities.

A Parachute is only necessary to go skydiving twice

This is the last class I teach at Brown as a graduate student (and most likely, ever). Amusingly, I taught it in the same room as the first course I taught as a graduate student. I've learned quite a bit about teaching inbetween, but in many ways it feels the same. Just like for students, the only scary class is the first one, although exams can be a real pain (to take, or to grade).

It's been a pleasure. As usual, if you have any questions, please let me know.

Leave a comment

Comment via email