At the recent Hot Topics Workshop on Murmurations, we talked about the phenomenon of murmurations of $L$-functions.

Murmuration Phenomenon

The murmuration phenomenon describes certain biases in averages of coefficients of elliptic curve $L$-functions. This begins with certain families $\mathcal{E}$ of elliptic curves, where each curve $E \in \mathcal{E}$ has an $L$-function of the shape^{1 1}I betray may analysis background in the notation, both in calling it $L(s, E)$ instead of $L(E, s)$ and in denoting the coefficients $a_E(n)$.

\begin{equation*} L(s, E) = \prod_p L_p(s, E)^{-1} = \sum_{n \geq 1} \frac{a_E(n)}{n^s}, \end{equation*}

where $L_p(s, E) \in \mathbb{Z}[p^{-s}]$ has degree $\leq 2$.

It turns out that often, the average of these coefficients when $n$ is prime has a consistent bias, that is

\begin{equation}\label{eq:murmuration} \mathbb{E}_{E \in \mathcal{E}}\; \big( a_E(p) \big) \end{equation}

is not random; these averages tend to particular values depending on $p$.

The shape of the families is relevant. For elliptic curves, the initial natural families were isogeny classes of elliptic curves with fixed rank, with conductors in a certain range $[N_1, N_2]$, or perhaps a dyadic range $[N, 2N]$. As $N$ in the dyadic ranges increase, the expected values of $a_E(p)$ appear to tend to a particular curve.

This set might not feel natural, but each specialization is very natural. Isogenous elliptic curves have almost everywhere the same $L$-function; thus choosing a single curve from each isogeny class doesn't omit much. And the parity of the rank is known to effect the number of points on elliptic curves (though the intuitive description of this effect is perhaps incorrect, as demonstrated in the murmuration phenomenon).

Since the first murmurations of elliptic curves were identified, several other murmuration phenomena have been discovered. The focus of the workshop was to try to identify explanations and further directions of inquiry.

Nonarithmetic murmurations

We can ask whether the murmuration is an arithmetic phenomenon or an analytic phenomenon. The most studied cases are all arithmetic so far: elliptic curves, modular forms, and Dirichlet characters.

Maass forms provide a non-arithmetic source of $L$-functions. My Maass form co-computer and collaborator Andrei Seymour-Howell and I were both attending and we have various types of Maass forms computed and sitting in our hard drives. Along with Kumar Murty, Peter Sarnak, and several others, we sought to experiment with Maass form murmurations.

We ask: are there murmations of Maass forms?

To investigate, we use our largest set of data: weight $0$, level $1$ Maass forms with eigenvalue parameter $R$ tending upwards. In analogy to elliptic curves, we might expect that the parity of the Maass form (which amounts to the root number or the precise shape of the functional equation) to have an effect. Thus we consider families of Maass forms $\mathcal{M}^{\pm}([R_1, R_2])$ consisting of level $1$, weight $0$ Maass forms with given $\pm$ parity and whose eigenvalue parameter $R \in [R_1, R_2]$.

Precisely, a Maass form of weight $0$ and level $1$ will have an expansion of the form \begin{equation*} f(z) = \sum_{n \geq 1} a_f(n) \sqrt{y} K_{iR}(2 \pi \lvert n \rvert y) \mathrm{cs}(2 \pi n x), \end{equation*} where $\mathrm{cs}(x)$ is either $\sin(x)$ or $\cos(x)$ depending on whether the Maass form is odd or even, respectively, and $K_{\nu}(x)$ is the modified $K$-Bessel function (sometimes called of third kind).

To investigate if we have a murmuration phenomenon, we look at points \begin{align}\label{eq:maassmurmur} &\mathbb{E}_{f \in \mathcal{M}^{\pm}([1.25^\ell, 1.25^{\ell+1}])} \; \big( a_f(p) \sqrt{p} \big) \\ &\qquad = \frac{1}{\# \mathcal{M}^{\pm}([1.25^\ell, 1.25^{\ell+1}])} \sum_{f \in \mathcal{M}^{\pm}([1.25^\ell, 1.25^{\ell+1}])} a_f(p) \sqrt{p} \notag \end{align} for increasing values of $\ell$. We do this separately for even ($\mathcal{M}^+$) and odd ($\mathcal{M}^-$) forms in the plots below.

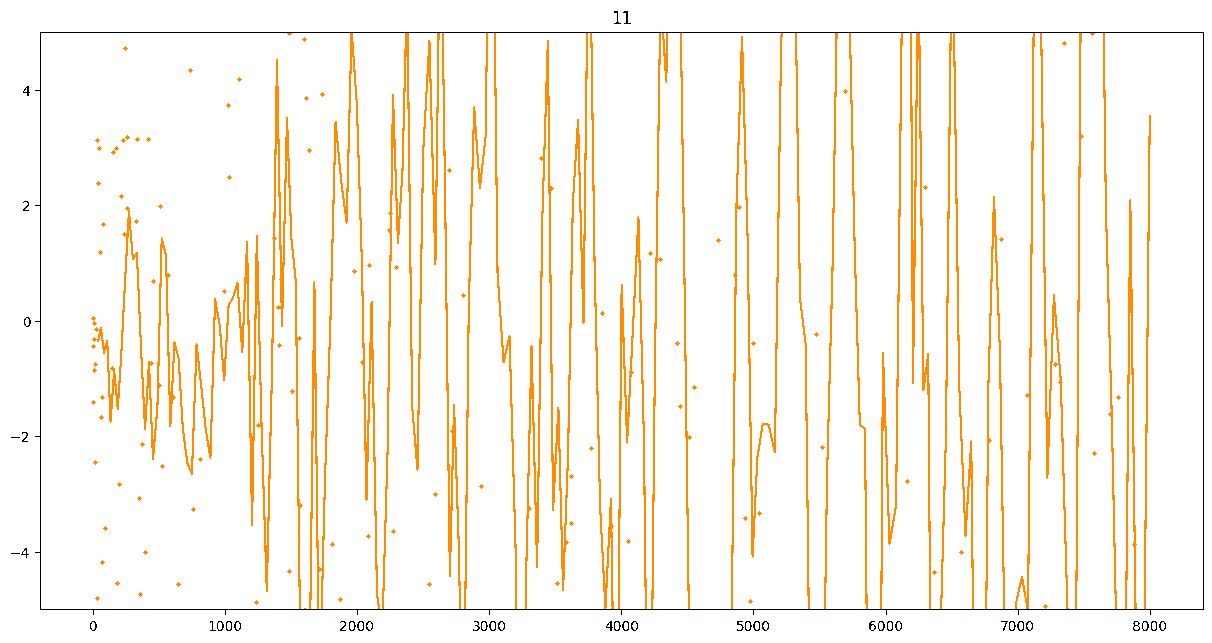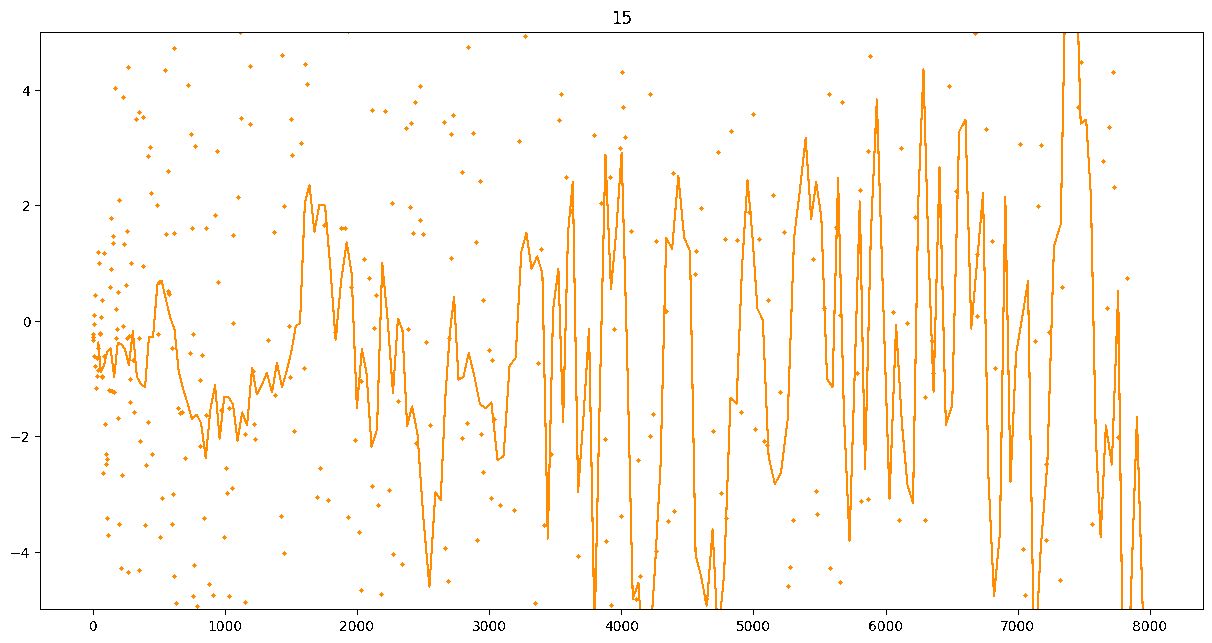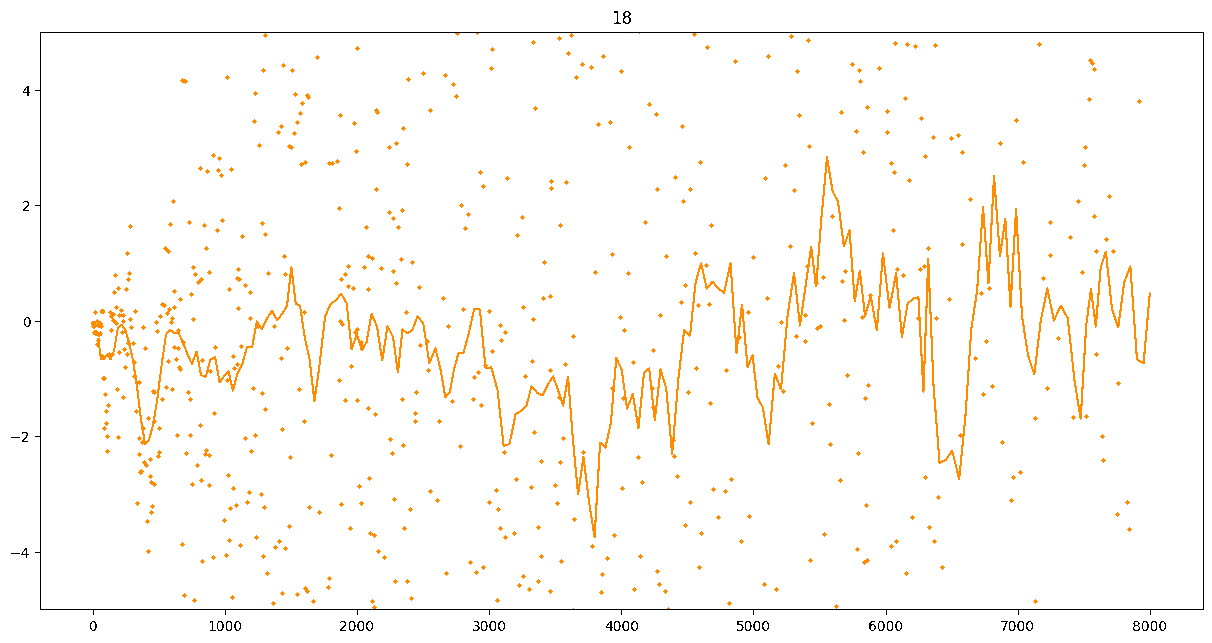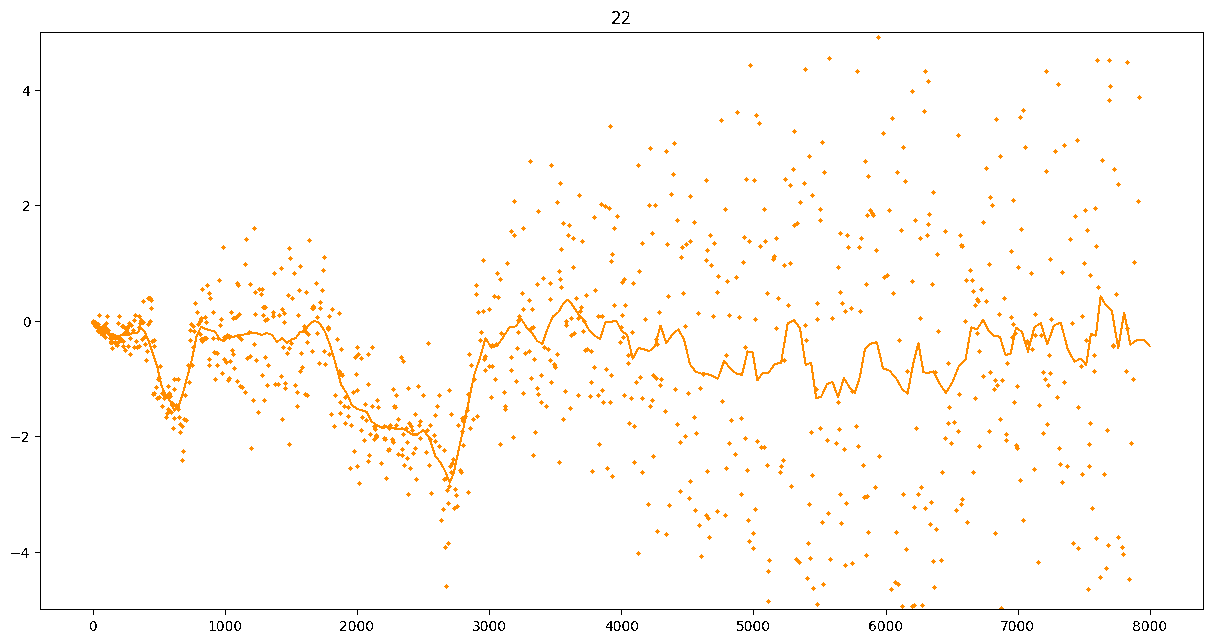
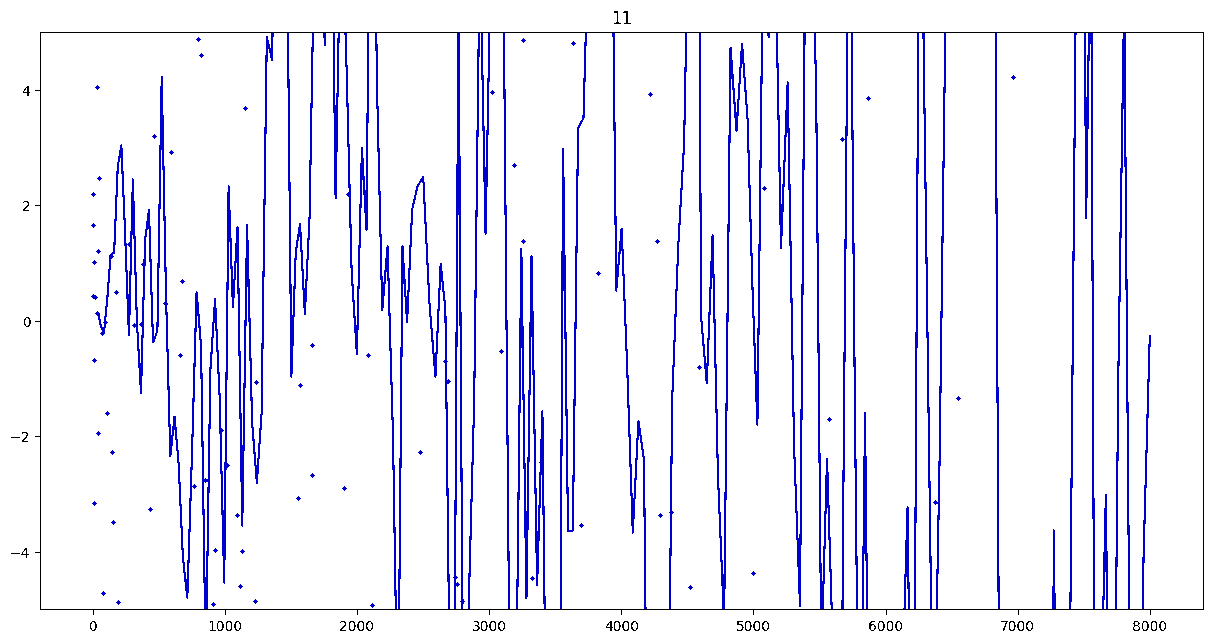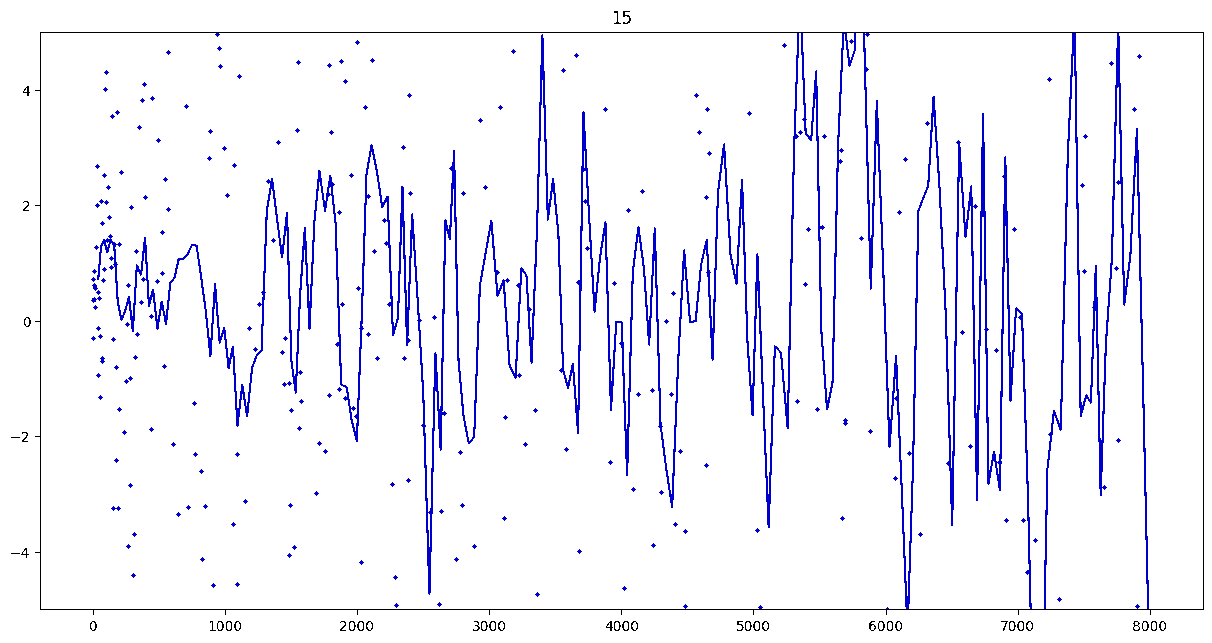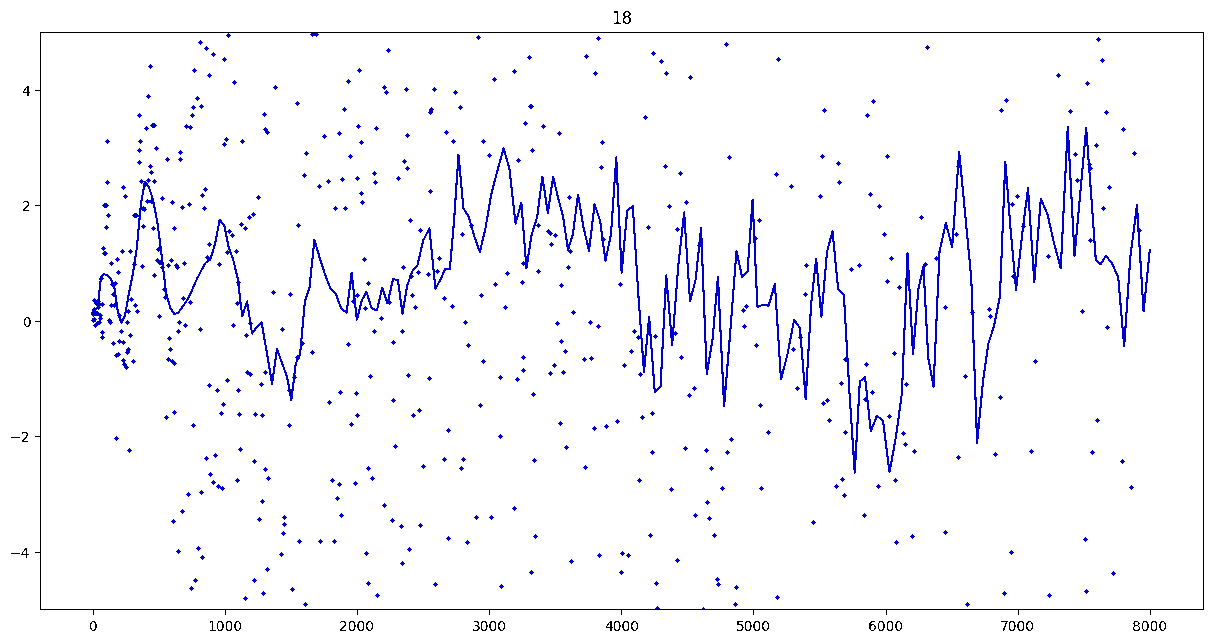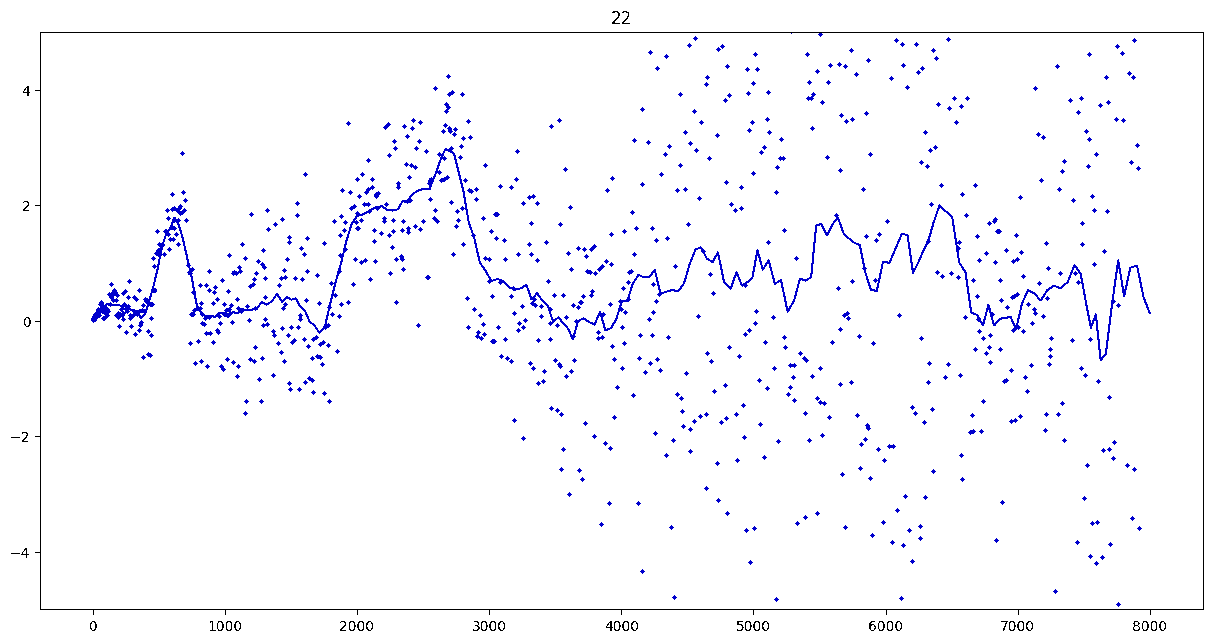
These plots include data from all Maass forms with eigenvalue up to approximately $30000$ (with eigenvalue parameter up to about $180$).

Several patterns announce themselves when these two sets of points are plotted together. Here, blue = even and orange = odd.^{2 2}As apocryphally said in murmurations, blue is always on top... until it's not.

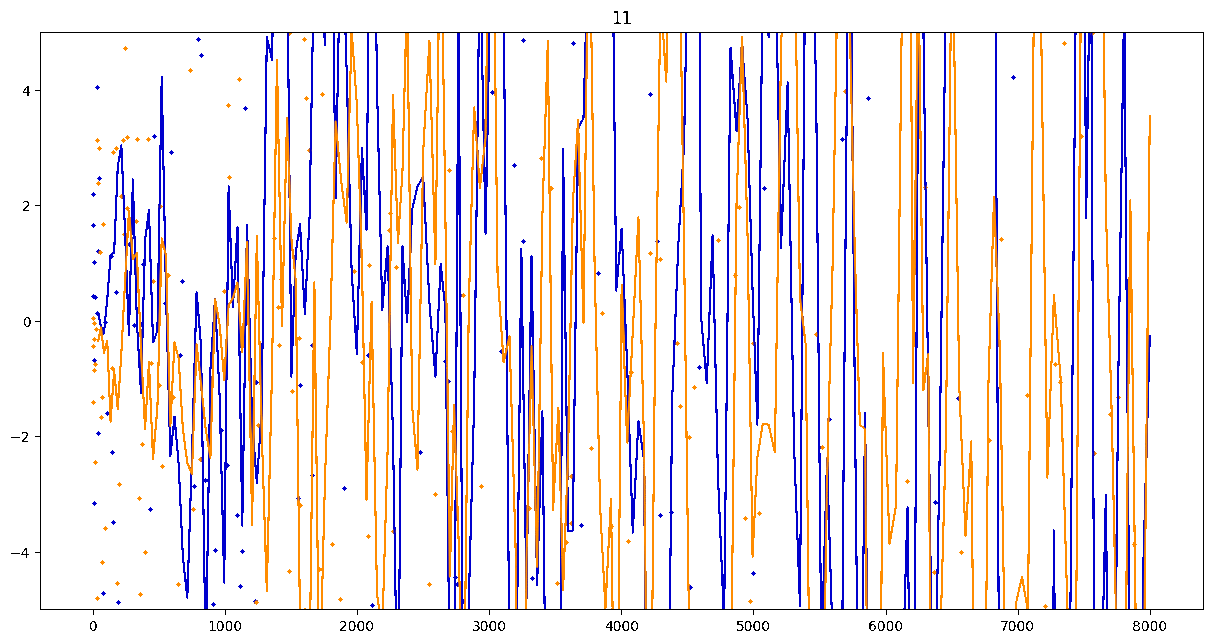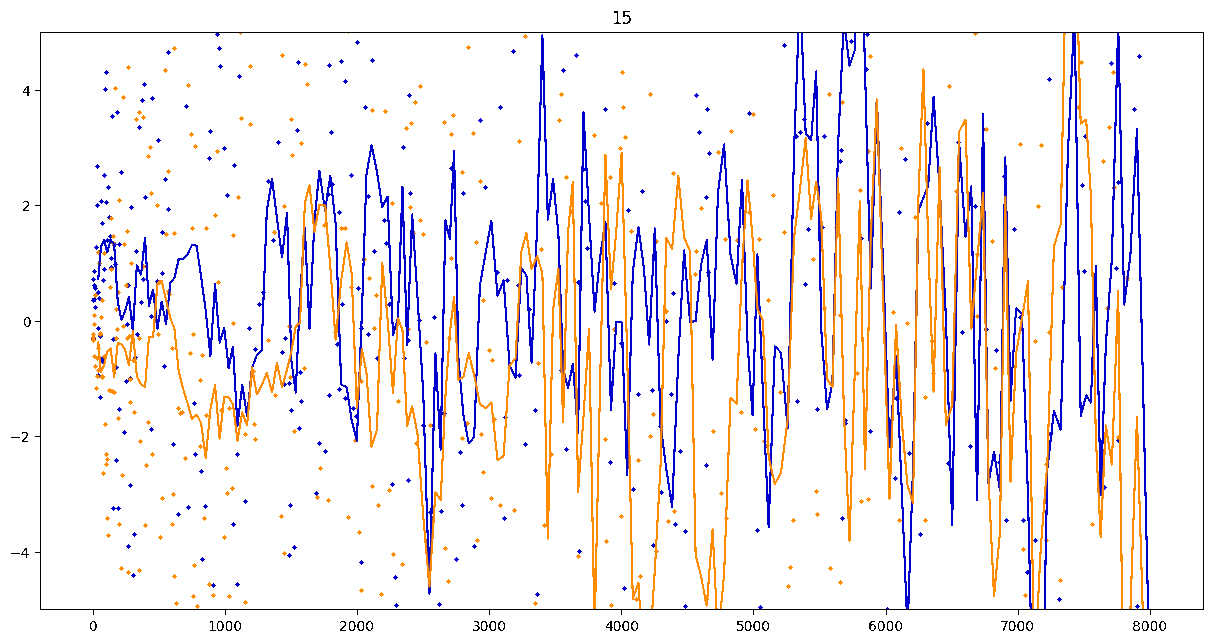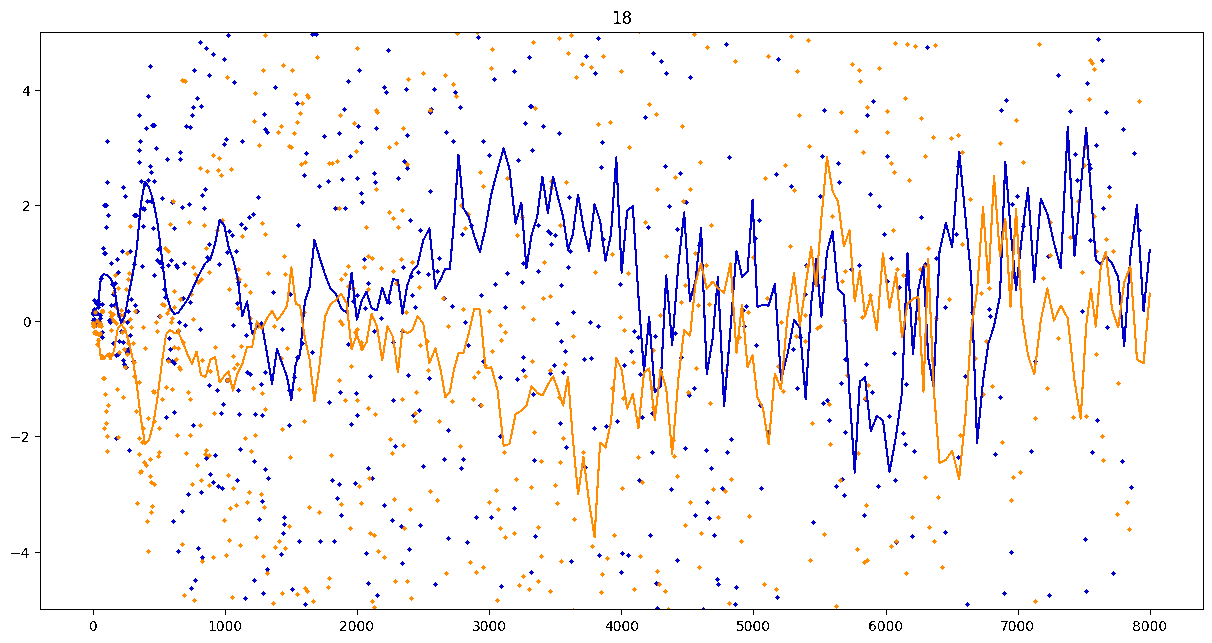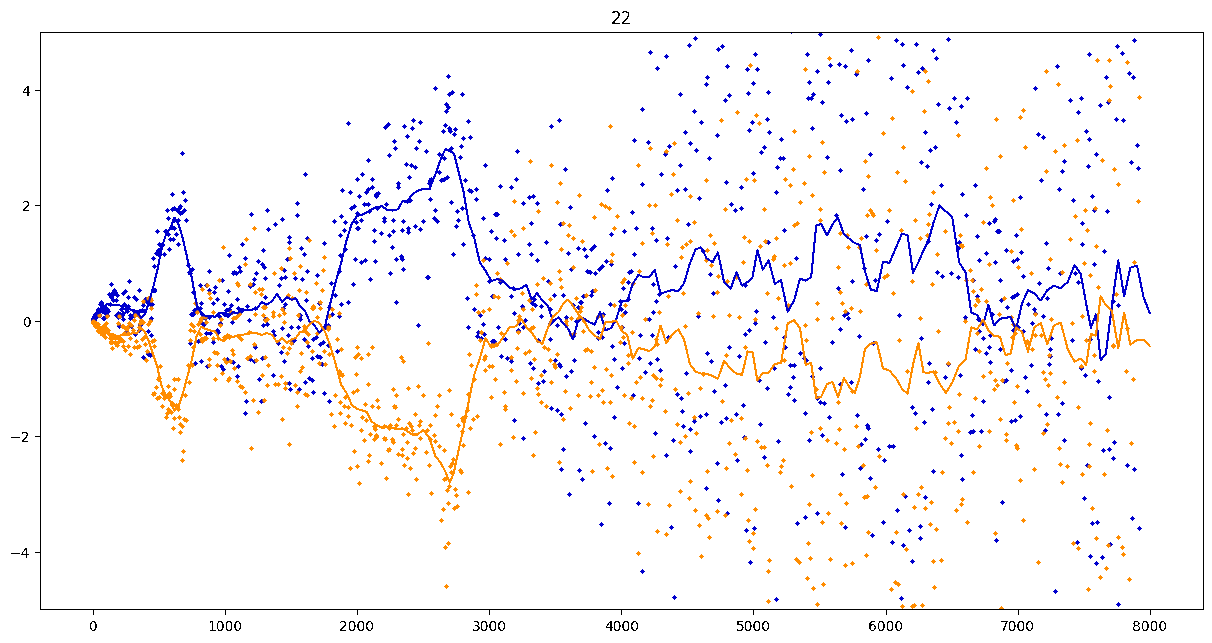
Patterns in the Plots

These plots suggest a murmurations phenomenon in Maass forms. Murmurations are perhaps nonarithmetic, and instead analytic.^{3 3}In some sense, it appears that they are shadows of various trace formulas.

Here are the last three frames.

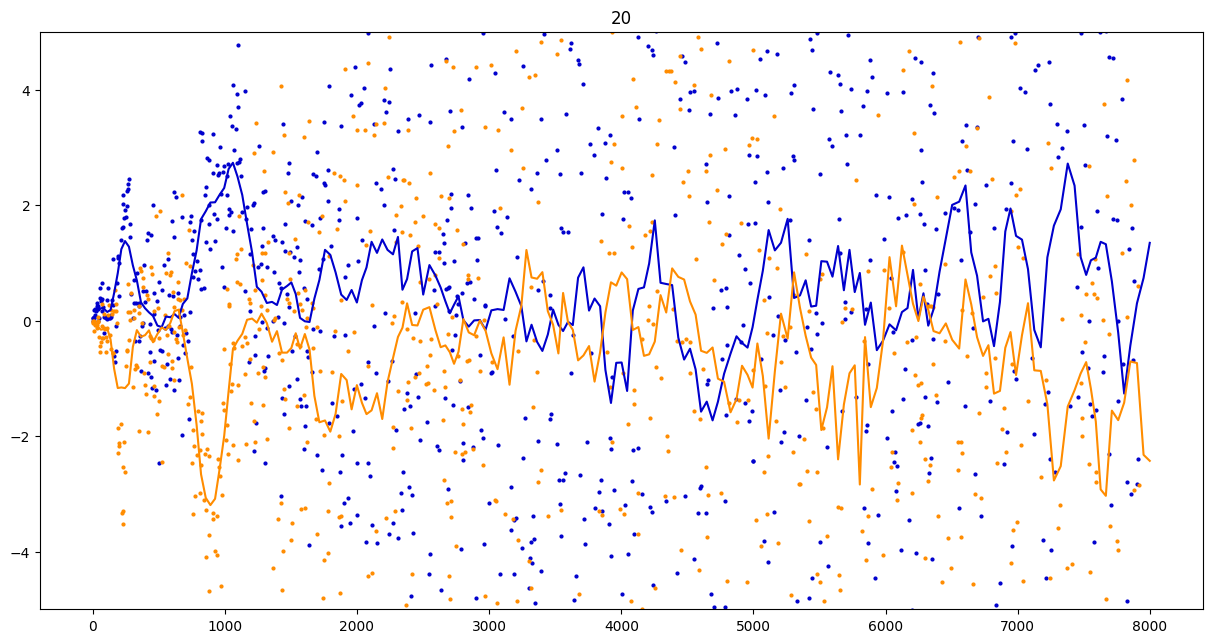
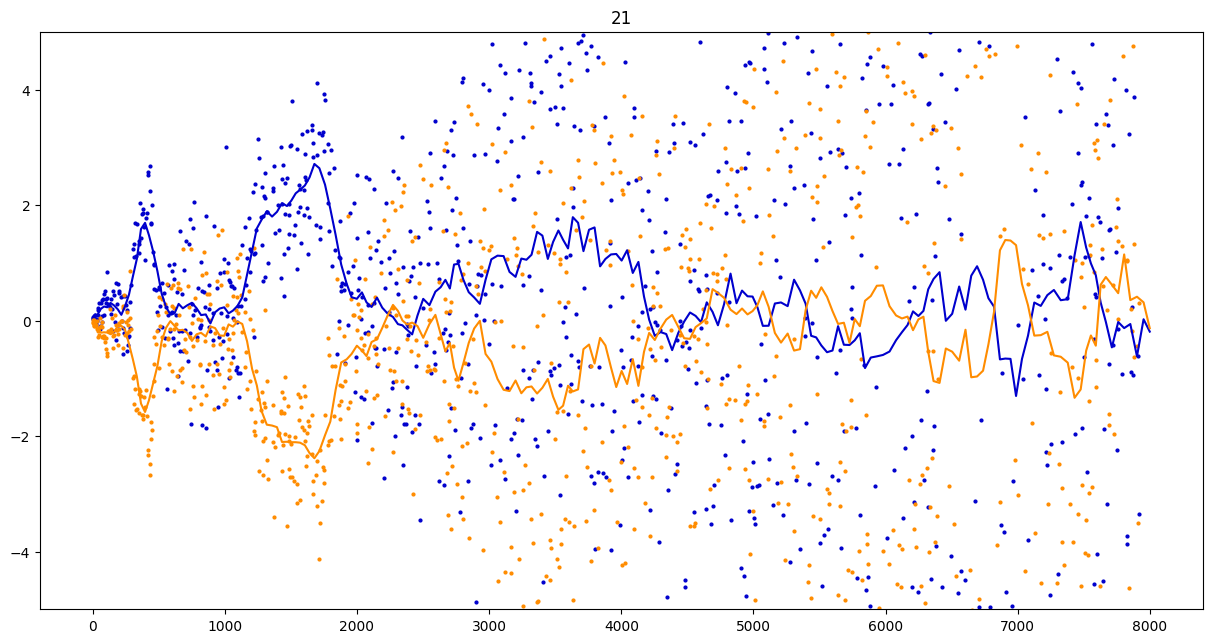
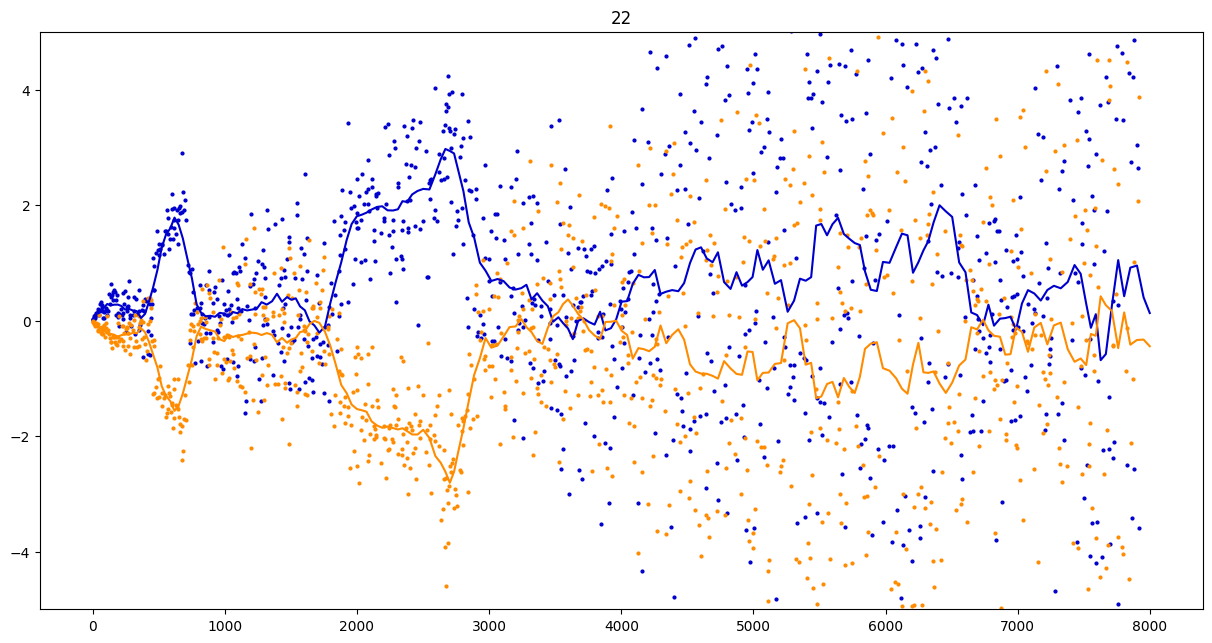
Some observations:

1. It seems that the averages are tending to a particular shape. As with other murmuration phenomena, the coherence increases in larger multiplicative ranges, but decreases as $p$ increases.
2. The parity of the Maass forms leads to similar but oppositely signed murmurations.

3. The current murmurations appear to be travelling waves. This suggests that they are incorrectly normalized.

   This is consistent with Jonathan Bober's observation that murmurations seem to describe behavior not as averages over certain primes, but instead as averages over coefficients near $p/Q$, where $Q$ is the conductor.

   I intend on returning to this later and seeing if a different normalization stabilizes the travelling wave. In a different note, I intend on describing a different set of observations on murmurations for holomorphic modular forms (with Bober, Booker, and Seymour-Howell) that also supports the $p/Q$ observation.

An alternative sum from Kuznetsov

A similar sum of coefficients of Maass forms appears in the Kuznetsov trace formula. We state this now.

Define the Kloosterman sum by \begin{equation*} S(m, n; c) := \sideset{}{'}\sum_{d \bmod c} e\Big(\frac{md + n\overline{d}}{c}\Big), \end{equation*} where the primed summation indicates that the sum is over residue classes $d$ prime to $c$, and where $d \overline{d} \equiv 1 \bmod c$. For any sufficiently nice even, holomorphic function $h$, we define \begin{equation*} k^*(x) = \frac{i}{\pi} \int_{-\infty}^{\infty} \big(J_{2 i r}(x) - J_{- 2 i r}(x) \big) \frac{r h(r)}{\cosh(\pi r)} \, dr. \end{equation*}

Then the Kuznetsov trace formula (for level $1$, weight $0$) says that \begin{align*} &\sum_{j = 1}^\infty \frac{h(r_j)}{\cosh(\pi r_j)} \rho_j(n) \overline{\rho_j(m)} + \frac{1}{\pi} \int_{-\infty}^\infty \frac{ (n/m)^{it} \sigma_{-2it}(n) \sigma_{2it}(m) } { \lvert \zeta(1 + 2it) \rvert^2 } h(t) \, dt \\ &\qquad = \sum_{c = 1}^\infty \frac{S(m, n; c)}{c} k^*(4 \pi \sqrt{mn} \; / c) + \frac{4}{\pi} \delta_{[m=n]} k(0). \end{align*}

Here, the coefficients $\rho_j(n)$ are the $n$th coefficients of the $j$th Maass form (which has eigenvalue $\frac{1}{4} + r_j^2$), normalized so that the Maass form has norm $1$.

After choosing $m = 1$, this gives an expression for \begin{equation*} \sum_{j \geq 1} \frac{\rho_j(n)}{\cosh(\pi r_j)} h(r_j). \end{equation*} Choosing $h$ to be essentially a bump function on certain intervals and squinting a bit, this looks like \begin{equation} \sum_{j \geq 1} a_f(n) w_f \end{equation} for a set of weights $w_f$ — very similar to \eqref{eq:murmuration} and \eqref{eq:maassmurmur}.

On this last note, Kumar Murty wrote down a short note containing the Kuznetsov trace formula statement. This is available here.^{4 4}And as the date might suggest, I didn't upload this particularly quickly.

Ongoing Research and Discussion

There are several things to examine further here!

I will continue to act as a fulcrum this, and I welcome discussion. If you would like to add something, send me an email or comment here (which still amounts to sending me an email in a certain way).

Leave a comment

Comment via email