The current issue of the Proceedings of the Royal Society A1 1covering mathematical, physical, and engineering sciences, as opposed to the "B" Proceedings, which covers biological sciences features cover artwork made by Vikas Krishnamurthy, Miles Wheeler, Darren Crowdy, Adrian Constantin, and me.

A version of the cover pre-addition is the following.

This is based on the work in A transformation between stationary point vortex equilibria, which concerns solutions to Euler's equation for inviscid (2D) fluid motion $$ \frac{\partial \mathbf{V}}{\partial t} + (\mathbf{V} \cdot \nabla) \mathbf{V} = - \frac{\nabla p}{p_0}, $$ where $\nabla = (\partial/\partial x, \partial / \partial y)$ is the 2D gradient operator. There is a notion of vortices for these systems, and the paper examines configurations of point vortices under certain idealized conditions that leads to particularly nice analysis. In the situation studied, one can sometimes begin with one configurations of point vortices and perform a transformation that yields another, bigger and more complicated configuration.
This is the situation depicted on the cover — begin with a simple configuration and iterate the process. The spiral shape was added afterwards and doesn't describe underlying mathematical phenomena. The different colors of each vortex shows whether that vortex is a sink or a source, essentially.
I was told most of this after the fact by Miles — who researches fluid dynamics, is a friend from grad school, and was my coauthor on a paper about the mean value theorem. I do not typically think about fluid dynamics (and did not write the paper), and it's a bit funny how I got involved in the production of this cover. But it was fun, and we produced many arresting images. In the future Miles and I intend to revisit these images and better describe how the various aspects of the image describes and reflects the underlying mathematical behavior.
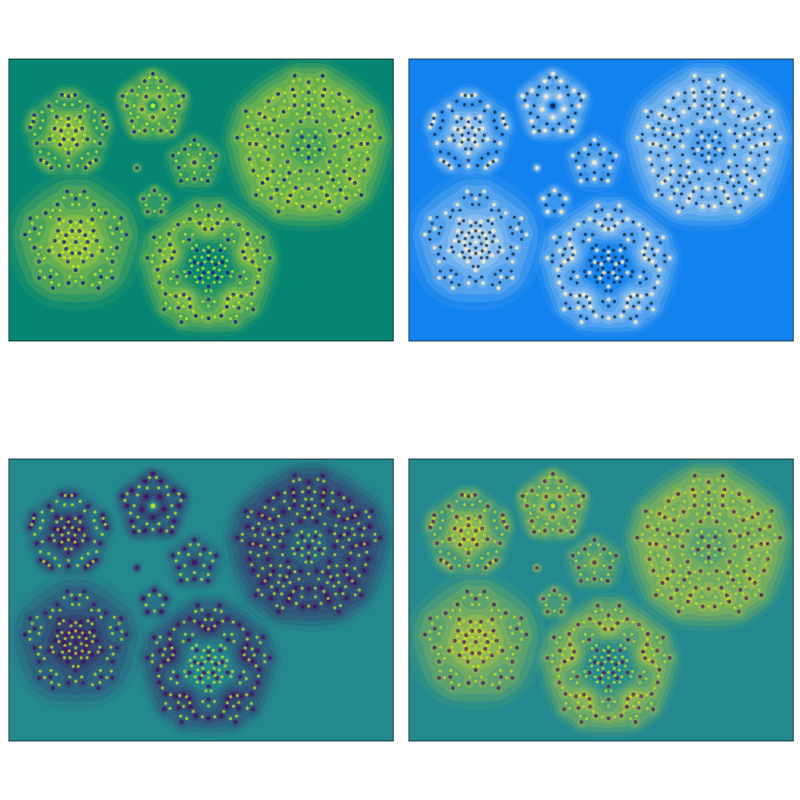
As a fun aside — we didn't only produce one image. We made many, and we made many configurations.2 2I should give an additional thanks to Miles, who spent a lot of time hand-tuning the particular parameters and contours in the final image. In my work on visualizing modular forms, I developed a few techniques for color selection from matplotlib style colormaps, and produced several variants. I've collected a few of these below.


Info on how to comment
To make a comment, please send an email using the button below. Your email address won't be shared (unless you include it in the body of your comment). If you don't want your real name to be used next to your comment, please specify the name you would like to use. If you want your name to link to a particular url, include that as well.
bold, italics, and plain text are allowed in comments. A reasonable subset of markdown is supported, including lists, links, and fenced code blocks. In addition, math can be formatted using
$(inline math)$or$$(your display equation)$$.Please use plaintext email when commenting. See Plaintext Email and Comments on this site for more. Note also that comments are expected to be open, considerate, and respectful.