I've posted a short note to the arxiv called "On Murmurations and Trace Formulas". (LD25c Knowl) This is an expanded version of my talk On Murmurations and Trace Formulas that I gave at the Simons Center for Geometry and Physics workshop on murmurations last November. The organizers of that workshop gathered several of the talks together for a special issue of the International Journal of Data Science in the Mathematical Sciences.
Several of my coauthors and collaborators were giving talks at that workshop, prompting me to give more of a speculative talk looking forwards instead of the standard talk describing some past work. I have given "typical talks" on my work in murmurations before. See my talk at LSU in November 2024 for my most recent.
Here, I want to further discuss an aspect that I think is commonly confusing in talks and the literature: the issue of normalization.
Algebraic and Analytic Normalization
The first murmurations observed were of elliptic curves, noting oscillatory behavior in averages of $a_E(p)$ across elliptic curves of conductor $\approx N$ against primes $p$, depending on the rank of the curve.
More precisely, for any conductor $N$, the average value of $a_E(p)$ across elliptic curves of ranks in $[N, 2N]$ and rank $\equiv \delta \bmod 2$ is predictable and (seems to) tend towards a well defined curve, or "murmuration function", $M_\delta(p/N)$. Further, it appears that $M_0(p/N) = - M_1(p/N)$.
This leads to the patterns in the frequently-cited murmuration plot.This is made to follow the plot in Murmurations of elliptic curves, https://arxiv.org/pdf/2204.10140, by He, Lee, Oliver, and Pozdnyakov.
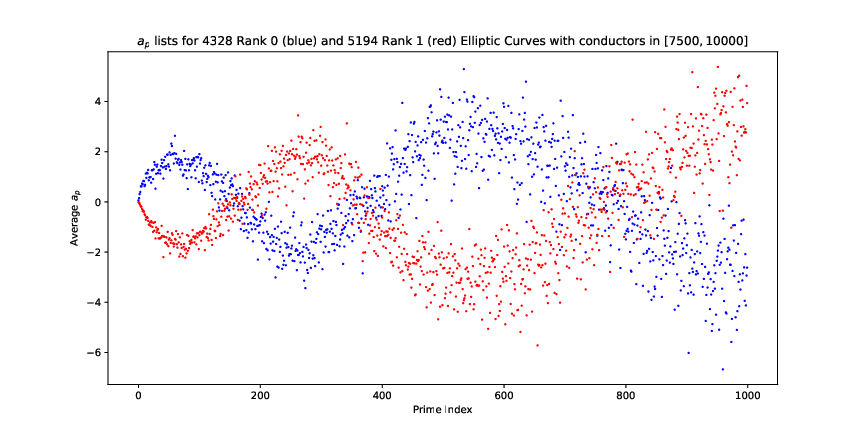
Implicitliy, the coefficients of the elliptic curves are normalized in the standard "algebraic" way. That is, the coefficients $a_E(p)$ are the traces of Frobenius, are integers, and vary between $-2\sqrt{p}$ and $2 \sqrt{p}$.
This normalization is natural with elliptic curves, but it appears that murmuration phenomena appear for many families of $L$-functions, which have a different natural normalization. Namely, it is naturally to normalize $L$-functions to have functional equations of the shape $s \mapsto 1 - s$. For elliptic curves, if we write the algebraic normalization as $a_E(p)$ and the analytic normalization as $\lambda_E(p)$, then these are related by $a_E(p) = \lambda_E(p) \sqrt{p}$.
When looking for murmurations in other families of $L$-functions, how should one normalize the $L$-functions?
Why do $a_E(p)$ values work so well?
Let's examine the elliptic curve case more closely. The coefficient $a_E(p)$ looks like a random number from $-2 \sqrt{p}$ to $2 \sqrt{p}$. It's not uniformly random. Instead these satisfy Sato-Tate and follow a circle-distribution. But nonetheless, when varying across families, the coefficients vary randomly in $[-2\sqrt{p}, 2\sqrt{p}]$. Adding $a_E(p)$ across several coefficients looks roughly like adding many numbers of size $\sqrt{p}$ together. When comparing across different conductor ranges, one looks at fixed ratios $p/N = c$, or equivalently at $p = cN$. Here, this means that we're adding many numbers of size $\sqrt{N}$ together.
But we're not summing absolute values. As the signs are fluctuating randomly from one curve to the next, the sum should experience some cancellation.1 1We'll return to how much cancellation in a moment. The effect is that that the extra coefficient size mostly counteracts the sign-change cancellation, giving a well-behaved overall sum.
Is $a_E(p)$ normalization necessary?
Having said that, what if we just don't use the algebraic normalization? What if we use only the analytic normalization? On the same data as the original murmuration plot, we get the following plot.
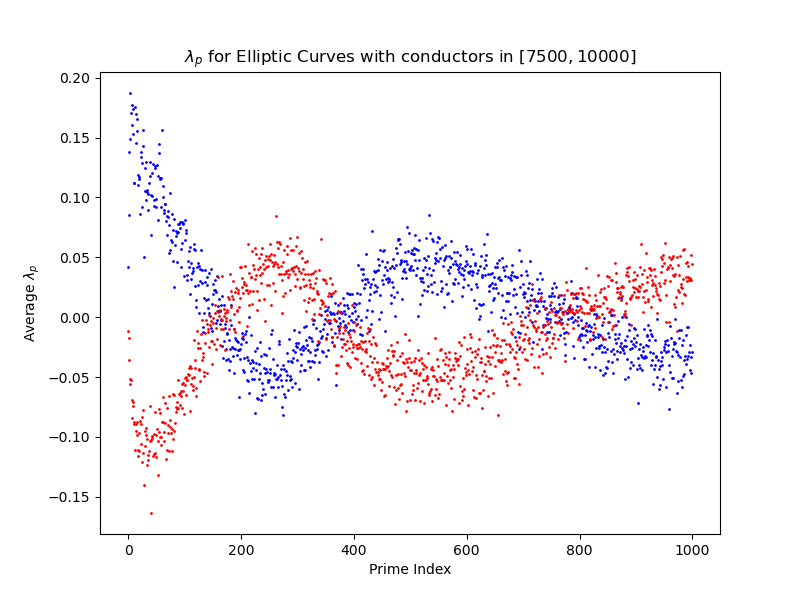
This clearly shows murmuration phenomena and has the same broad structure — with the one notable exception that the overall murmuration is decreasing in magnitude.
In my weight $k$ modular form murmuration paper and Maass form murmuration papers, we used the analytic normalization and correspondingly proved murmuration functions that were decaying. Nonetheless, all the data is there.
In short, I think there is an overemphasis on normalization.
Is the algebraic normalization the "best"?
Let's look closer at the sums. Suppose there are $X$ curves $E$ with conductor between $N$ and $2N$. It is conjectured2 2See Families of elliptic curves ordered by conductor by Shankar, Shankar, and Wang, https://arxiv.org/pdf/1904.13063, and the references there for more. that $X \sim c N^{5/6}$ for an explicit constant $c$. We assume this below.
Then we look at \begin{equation*} \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} a_E(p) \end{equation*} The central limit theorem suggests that the size of this sum should behave like \begin{equation*} \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} a_E(p) \asymp \sqrt{p} X. \end{equation*} Again, with murmurations we look at a fixed ratio $p/N = k$, or rather that $p \asymp N$. This implies that \begin{equation*} \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} a_E(p) \asymp N^{11/12}. \end{equation*} For murmurations, we divide by the number of curves $X \asymp N^{5/6}$, and thus we expect that the murmuration sum (in algebraic normalization) behaves like \begin{equation} \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} a_E(p) \asymp N^{11/12} / N^{5/6} \asymp N^{1/12}. \end{equation}
That is, we should expect the murmuration function to grow slightly in $p/N$! (Maybe if we look closely at the original murmuration plot, this seems true... but it seems likely that this affect is less than the "fuzz" or "snow" effects).
If we want constant size murmurations, then this suggests the "correct" normalization of looking at \begin{equation*} \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} a_E(p) / p^{1/12} = \sum_{\substack{E \\ \mathrm{N \leq \mathrm{cond}(E) \leq 2N}}} \lambda_E(p) p^{5/12}. \end{equation*}
This would give the following.
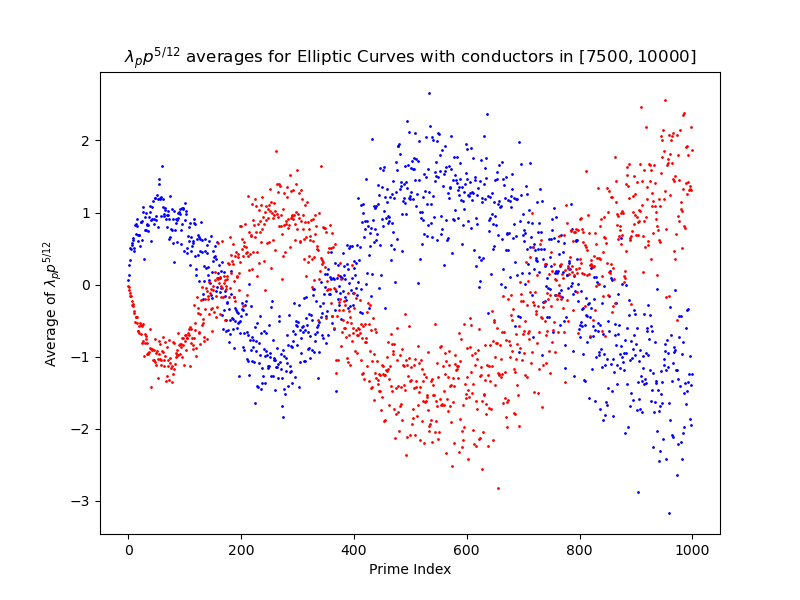
In principle, it could be informative to compare to the standard $a_E(p)$ plot, including the expected lines of growth there. This looks like
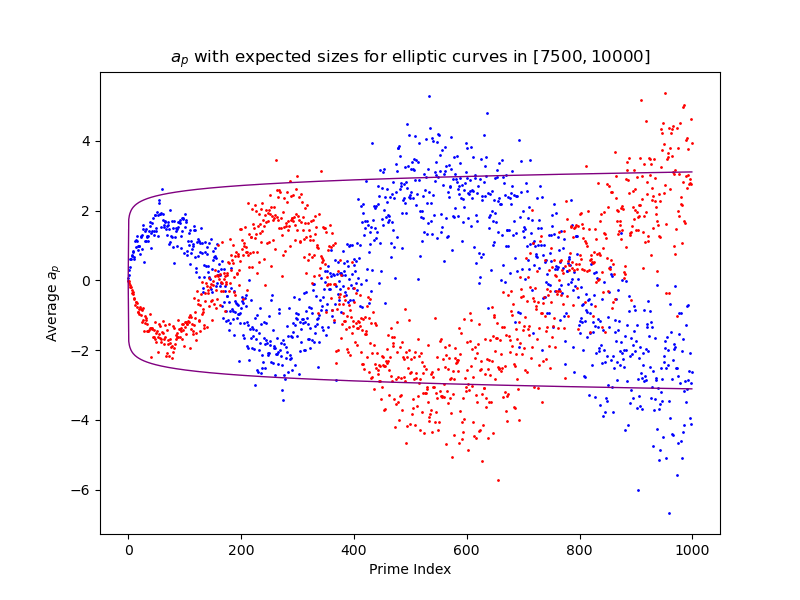
The expected growth $p^{1/12}$ is shown. It's hard to say if this looks right or not. The fuzz is a problem. In practice, the difference is very slight. It turns out that $X^{1/12}$ grows pretty slowly.
The size of the family played an important role in this discussion! The "correct" normalization for modular forms of weight $2$ and varying level would be $\lambda(p) \sqrt{p}$, as in that case the number of modular forms of conductor $N$ is $\asymp N$.
But the point remains that perfectly normalizing the coefficients so that the murmuration function is constant on average isn't important!
Info on how to comment
To make a comment, please send an email using the button below. Your email address won't be shared (unless you include it in the body of your comment). If you don't want your real name to be used next to your comment, please specify the name you would like to use. If you want your name to link to a particular url, include that as well.
bold, italics, and plain text are allowed in comments. A reasonable subset of markdown is supported, including lists, links, and fenced code blocks. In addition, math can be formatted using
$(inline math)$or$$(your display equation)$$.Please use plaintext email when commenting. See Plaintext Email and Comments on this site for more. Note also that comments are expected to be open, considerate, and respectful.