There was a quiz this week - in this post, we consider the solutions, common mistakes, and the distribution.
The quiz was as follows:
A girl flies a kite that stays a constant 200 feet above the ground. The wind carries it away from her at 20 feet per second. We were first to draw a picture.
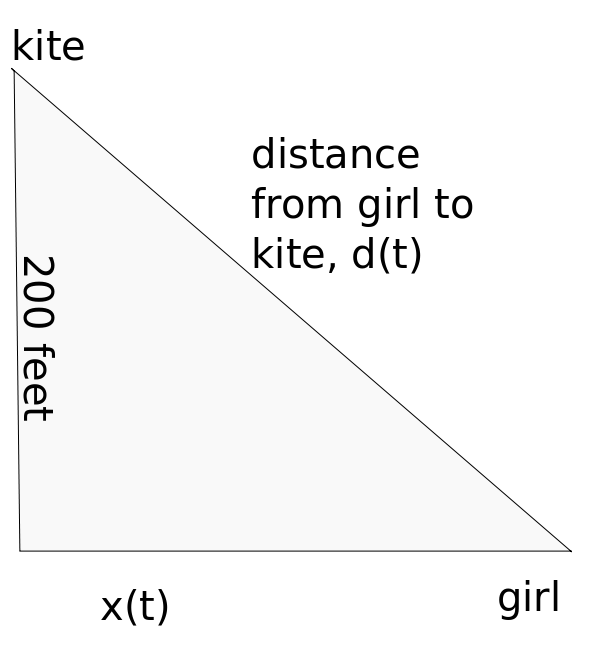
I have included a picture at the right, excluding the initial position (which is not really useful to this problem). In addition, we know that $x'(t) = 20$. Almost everyone drew the picture correctly, so I won't belabor this point too much.
We were then asked to give an equation for the square of the distance from the girl to the kite. The question explicitly asks for the square of the distance. This is a right triangle, so we write $d(t)^2 = 200^2 + x(t)^2$, from the Pythagorean Theorem.
Finally, we were asked to compute the rate at which the girl must let out string when the kite was 300 feet away from the girl. The most common (and often, only) mistake on the test was to interpret this to mean that $x = 300$ at this time. But the distance between two things is the length of the straight line between them unless stated otherwise, so we actually care about the time when $d = 300$.
So we have a triangle with hypotenuse $300$ and one leg $200$, so the other leg is of length $\sqrt{300^2 - 200^2}=100 \sqrt 5=x$.
Now we put it all together. From $d(t)^2 = 200^2 + x(t)^2$, we differentiate to get $2d(t)d'(t) = 2x(t)x'(t)$. We are looking to find $d'(t)$ when $d(t) = 300$, and we found that at this time $x(t) = 100\sqrt{5}$. We also know that $x'(t) = 20$ at all times. Plugging these in, we get that $2 \cdot 300 \cdot d'(t) = 2 \cdot 100\sqrt 5 \cdot 20$, or that $d'(t)=\dfrac{200 \sqrt 5 \cdot 20}{600} = \dfrac{20 \sqrt 5}{3}$ feet per second.
The class did really, really well on this quiz. I was impressed. The vase majority of the class made at least an 8. The only mistake on average was to mistake which leg was implied by "distance from the kite to the girl."
Info on how to comment
To make a comment, please send an email using the button below. Your email address won't be shared (unless you include it in the body of your comment). If you don't want your real name to be used next to your comment, please specify the name you would like to use. If you want your name to link to a particular url, include that as well.
bold, italics, and plain text are allowed in comments. A reasonable subset of markdown is supported, including lists, links, and fenced code blocks. In addition, math can be formatted using
$(inline math)$or$$(your display equation)$$.Please use plaintext email when commenting. See Plaintext Email and Comments on this site for more. Note also that comments are expected to be open, considerate, and respectful.