mixedmath

First and foremost: There is a quiz next week during recitation! What is it over? you might ask. Any material from any of the first three homework sets (i.e. all material covered in lecture up to Tuesday September 25th) will be fair game.

Someone asked me in office hours this week: "Why do you end your posts with something about a 'fold'?" I mention a 'fold' to indicate that there is more to the post, and that you should click on the name of the post or on the not-so-subtle (more...) at the bottom for the rest. Fittingly, the rest is after the fold:^{1 1}This made more sense pre site-reorg.

We had three questions in recitation.

1. Compute the following limits:
   1. Given that $\frac{1}{2} - \frac{x}{6} \leq \frac{e^{-x} + x - 1}{x^2} \leq \frac{1}{2}$ for small $x$, evaluate $\lim_{x \to 0} \dfrac{e^{-x} + x - 1}{x^2}$
   2. $\lim_{x \to 0} \dfrac{\sin x}{x} $ with justification.
2. Consider the function $f(x) = \dfrac{2x^2}{\sqrt{4x^2 - 7} - \sqrt{7}}$.
   1. What is the domain of $f(x)$?
   2. What is $\lim_{x \to 0} f(x)$?
   3. Can $f(x)$ be "extended" to a continuous function of all of the real line?
3. Cookie dough is poured into Purgatory Chasm at a rate of $3t^2$ gallons after $t$ hours.
   1. What is the average rate of cookie dough pumped per hour between $t = 2$ and $t = 4$ hours?
   2. What is the average between $t = 2$ and $t = 3$ hours?
   3. What is the "instantaneous" rate of flow at $t = 2$ hours?

It seemed that a lot of people had a bit more trouble with this than last week, which is fine! And one of these is a whole lot harder than the other two. Let's look at the solutions:

Question 1

This question is designed around the sandwich theorem. This says that if $g(x) < f(x) < h(x)$ and $\lim_{x \to c} g(x) = \lim_{x \to c} h(x) = L$ (note both the lower and upper bounds), then we must also have that $\lim_{x \to c} f(x) = L$. It's literally 'sandwiched' between the lower and upper bounds, so it has nowhere to go.

So to do the first question, we see that it's been delivered to us. Noting that the limit of the lower and upper functions are both $\frac{1}{2}$, we conclude by the sandwich theorem that our limit is also $\frac{1}{2}$.

As for the second part, it's not at all immediately obvious that we use the sandwich theorem to do this. In fact, it's not at all clear how to do this at all. So I helped set it up. Let's look at the setup now, too.

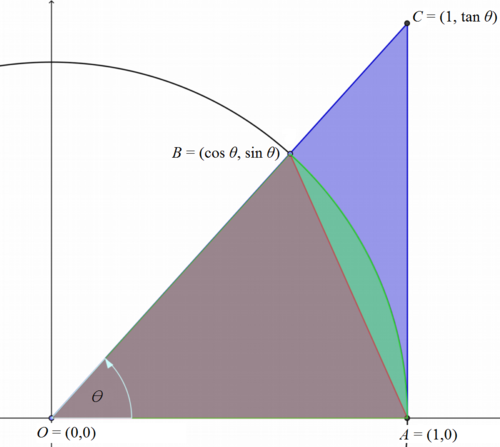
The picture of what's going on is above, and it builds off of what we know from our unit circle. We use the sandwich theorem on the areas at the right. In particular, the area of the brown triangle is $\frac{1}{2} \cos \theta \sin \theta$. The area of the pie-piece containing both the brown and the green parts is $\frac{1}{2} \theta$ (do you remember why?). The area of the large triangle, including the brown, green, and blue is $\frac{1}{2} \tan \theta$.

Thus for small $\theta$, we have that $\sin \theta \cos \theta < \theta < \tan \theta$. I would like to divide through by $\sin \theta$, but a complication arises: what if it's negative?

So we first compute $\lim_{\theta \to o^+} \dfrac{\sin \theta}{\theta}$, where since I've restricted to positive and small $\theta$, I know that $\sin \theta$ is positive. Then I know that

$\cos \theta < \dfrac{\theta}{\sin \theta} < \dfrac{\tan \theta}{\sin \theta} = \dfrac{1}{\cos \theta}$

But now we know that the limit of the left and right as $\theta \to 0^+$ is $1$, and so we know that $\lim_{\theta \to 0^+} \dfrac{\theta}{\sin \theta} = 1$.

Computing the left-hand limit yields $\cos \theta > \dfrac{\theta}{\sin \theta} > \dfrac{\tan \theta}{\sin \theta} = \dfrac{1}{\cos \theta}$ (the signs have flipped since we divided by a negative sine). But the same reasoning holds!

So we can conclude that $\lim_{x \to 0} \dfrac{\sin \theta}{\theta} = 1$. I'd like to point out that this is needed to understand the derivative of sine (and cosine, really). Some people were tempted to "use L'Hopital" (if you don't know what that means, don't worry - it's a more advanced calculus skill that we haven't gone anywhere near yet), but this requires knowing the derivative of sine, which requires this limit. In other words, that's circular! (get it? sine, circular?) So this is somehow good.

Question 2

There are many nice elements to this question. What is the domain? We see that the $x$ terms are squared within the square roots, so there will never be any negatives under the radicals. But we need to worry about the denominator of the fraction being zero, so we need $x \neq 0$. This gives us our domain: all $x$ such that $x \neq 0$.

To compute the limit, we "rationalize the denominator." In other words, we look at $\dfrac{2x^2}{\sqrt{4x^2 + 7} - \sqrt 7} \cdot \dfrac{\sqrt{4x^2 + 7} + \sqrt 7}{\sqrt{4x^2 + 7} + \sqrt 7}$. With this, we can compute the limit using the "obvious methods."

We get $\dfrac{2x^2 (\sqrt{4x^2 + 7} + \sqrt 7)}{4x^2} = \dfrac{4x^2 + 7} + \sqrt{7}{2}$. So when we take the limit as $x \to 0$, we get $\sqrt{7}$.

Now, when we ask "can we extend this function to a continuous function," we are asking if we can 'plug any holes.' Our function has a hole at $x = 0$, but our function also has a limit at $x = 0$. Recall that a function is continuous at a point if two things hold: the function has a value at that point, and the limit of the function at that point exists and is equal to that value. So if we define our function to be $\sqrt 7$ when $x = 0$, then we will have 'plugged our hole' and thus will have a continuous function of $x$.

Question 3

There were a few homework questions that were a lot like this question, and this was perhaps the most boring of the questions. If there is anything unclear, let me know and I'll expand this problem.

Remember that we have a quiz next week! And also feel free to come to my office hours, or those of Tom.

Leave a comment

Comment via email