When trying to machine learn the Möbius function for LD25b, I had a problem determining what the machine learning models were paying attention to. Let's recall the setup.
The Möbius function $\mu(n)$ is $0$ if $p^2$ divides $n$ for any prime $p$, and otherwise $\mu(n) = (-1)^{\omega(n)}$, where $\omega(n)$ is the number of prime divisors of $n$. Obvious methods of training ML models to predict $\mu(n)$ quickly learn to detect divisibility by squares of primes, but then don't seem to learn much of anything else.
I wanted to try to see if models could figure out something other than divisibility by squares. To do this, I chose a representation of $n$ that obfuscated square divisibility: write $n$ as the vector of the residues mod the first $100$ primes,
\begin{equation*} (n \bmod 2, n \bmod 3, n \bmod 5, n \bmod 7, \ldots, 541). \end{equation*}
After training models, I noticed that the behavior of the model closely agreed with the behavior of a model using only the inputs $(n \bmod 2, n \bmod 3)$ (the residue class mod $6$).1 1I hadn't realized before the experiments that the residue class mod $6$ is enough to strongly outperform naive strategies. In hindsight, this is clear. But how can one show this is actually what the model is paying attention to?
One of the reviewers of my paper suggested an extremely simple approach that I hadn't considered: feed the trained model deliberately corrupted inputs!
For example, if changing the residue mod $p$ has a strong effect on the predictions, then this suggests that $n \mod p$ is a very important feature. If it didn't change, then this suggests that $n \bmod p$ is not a very important feature.
Doing this shows the following.
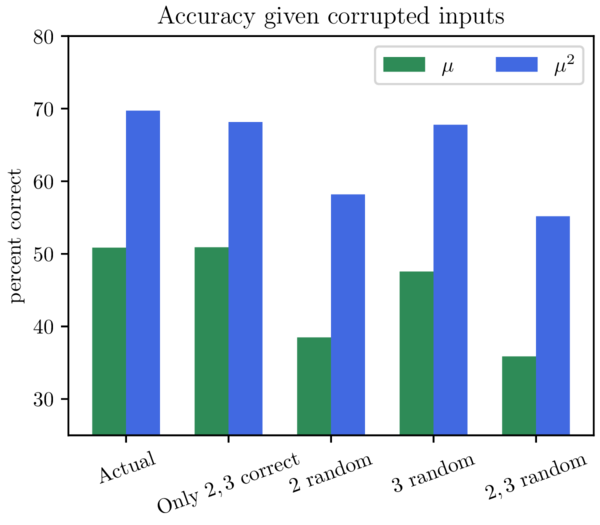
The left is the actual data with no corruption. Just beside it is the same model, but fed data where all but $(n \bmod 2, n \bmod 3)$ have been corrupted (and replaced by random inputs). Notice that the behavior is very similar, with almost no change in the quality of predictions for $\mu(n)$ and only a small decrease in predictive power for $\mu^2(n)$.
The remaining three show when $n \bmod 2$ is corrupted (high effect), when $n \bmod 3$ is corrupted (notable effect), and when both are corrupted (very high effect). Notably, when both $n \bmod 2$ and $n \bmod 3$ were corrupted, the overall model predictions became worse than the "trivial method" of predicting the largest data class (which is $0$ for $\mu(n)$ and $1$ for $\mu^2(n)$).
This strongly suggests that the model uses the residue class mod $6$ and almost nothing else.
This isn't the most powerful or accurate method of detecting feature importance in ML. But as it can be applied to any ML architecture, it's very broadly applicable.
Info on how to comment
To make a comment, please send an email using the button below. Your email address won't be shared (unless you include it in the body of your comment). If you don't want your real name to be used next to your comment, please specify the name you would like to use. If you want your name to link to a particular url, include that as well.
bold, italics, and plain text are allowed in comments. A reasonable subset of markdown is supported, including lists, links, and fenced code blocks. In addition, math can be formatted using
$(inline math)$or$$(your display equation)$$.Please use plaintext email when commenting. See Plaintext Email and Comments on this site for more. Note also that comments are expected to be open, considerate, and respectful.