mixedmath

This is a continuation of a previous post.

I've been following the two Coursera calculus MOOCs: the elementary introductory to calculus being taught by Dr. Fowler of Ohio State University, and a course designed around Taylor expansions taught by Dr. Ghrist of UPenn, meant to be taken after an introductory calculus course. I've completed the 'first week' of Dr. Fowler's course (there are 15 total), and the 'first unit' of Dr. Ghrist's course (there are 5 total), and I have a few things to say.

The beginning of each semester was a stressful time at Georgia Tech, my undergraduate university. The add/drop process for classes starts up again, but only lasts a little while. Whereas some universities have a 'shopping period,' where students can go to different classes and choose which classes they want to take, Georgia Tech does not. This was typically okay, because most of my classes were more or less ordained by my requirements (both those from the university and those I imposed on myself). But this also meant that when I went to class on those first days, it was not to see whether I was going to continue to take that class.

Instead, I used that time to form impressions about my professor, the other students, and how the class would run.

And often, I was wrong about my impressions. That's how I feel now, having completed the first portions of these two classes.

The first thing to notice about Dr. Ghrist's class is that it looks cartoony. If I were being frank, I'd say it looks garish. I sort of expected this, because I was already familiar with Dr. Ghrist's FLCT: Funny Little Calculus Text. This is a booklet that was once freely-available (and now is $0.50 printable from googleplay). It's only 45 pages or so, and is a semi-humorous and semi-instructional set of lecture notes. This style of presentation does not appeal to me.

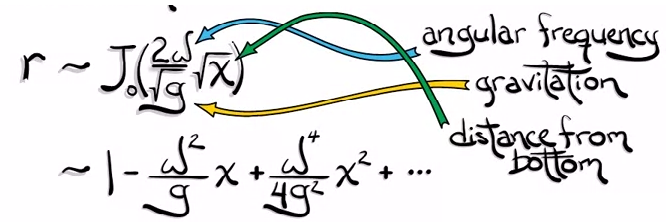
Above, I've given an example (taken from one corner of his lectures on Coursera). This example is special because most of the text is black (a very hard-to-find example).

Perhaps a more typical example looks like the following:

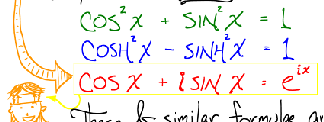
That's my major complaint about the course so far (I do not expect it to change). There's a wiki attached to the course that contains the text of the lectures written in good old black sans serif fonts on a white page, thank goodness. Further, this wiki serves as the only text of the course (good in that Dr. Ghrist isn't forcing his students to spend a nominal fee on his book, bad in that there is no additional perspective to be gained). But it would be wrong for me to omit the fact that Dr. Ghrist has clearly spent an enormous amount of time preparing each lecture (and their custom, hand-drawn pictures and fonts). The level of the presentation is very clean (aside from the painful visuals themselves).

Other than that, the course starts with Taylor series and uses them as their fundamental building block. He derives l'Hopital's rule using Taylor series (not atypical) and considers many limits that require Taylor series rather than l'Hopital's rule to compute (pretty atypical). He takes what I've come to view as a very applied viewpoint, dealing with many partial Taylor expansions and taking these through function operations and compositions. Students who do well in his first section will likely be better at this sort of series manipulation then students coming out of any calculus course covering Taylor series that I've ever taken or taught. But there is a cost: Dr. Ghrist has not yet considered any error terms. So even though students become very good at manipulating finite Taylor polynomials, they have not considered at all any error, change in error, or propagation of error.

In fact, Dr. Ghrist's class is almost completely devoid of asking why? At the start, it's stated that $e^x = 1 + x + x^2/2! + \ldots$, and that $e^{i \theta} = \cos \theta + i \sin \theta$, and so on. But there is no justification given for anything. And that's not necessarily bad - many times, when I've taught, students' eyes glaze over when being taught any 'theory.' One of the worst artifacts of a rigorous teaching past in modern calculus classes are ideas related to proofs that students are expected to not understand, or use, or perhaps even be exposed to. For example, in the Math 90 class that I was just involved in, not all the teachers got around to actually teaching why the Fundamental Theorem of Calculus was true (i.e. giving the proof). But students still computed left endpoint, right endpoint, etc. finite Riemann sums. Now, they never actually compute, or even reasonably estimate, any worthwhile integral using these. They instead just multiply and add a few sets of numbers together.

There is no understanding gained from this. Instead, it's a tedious chore. I'm not saying that Riemann sums should not be taught - I'm saying they should either be taught and used (like to numerically estimate worthwhile integrals or to understand the FTC) or not taught at all.

Dr. Ghrist has chosen the not-taught-at-all parallel in his course. So every result he mentions comes from either some arithmetic manipulations using facts-from-God (i.e. ideas with no clear origin, but instead simply handed down from the Teacher), or by incorporating additional facts-from-God. This may sound bad, but this is essentially how most primary and secondary math education is taught in the States (for better or worse). In this way, Dr. Ghrist seems to aim his course at students with what I have come to think of as a high-school level of commitment. (In this way, it's similar to how the Calculus courses at Brown are taught - advanced arithmetic without much emphasis on proofs and no emphasis on proof techniques or student-driven proofs, and weekly homework sets)

Dr. Ghrist structures his course to be a series of roughly 15-minute-or-less videos. And to each video, there is a corresponding homework problem. I find the homeworks to be very-well written, and hard. But each students can attempt them as many times as they like. There's an aspect of the course that I love, which is that the answers to the homeworks are not given out. Thus if you miss a question, you can go back and try again, but you must find your own mistake (or go to the discussion forums). The 'obvious' alternative is to give out explanations to certain questions to answer why the correct answer is, in fact, the correct answer (which happens to be the model used in Dr. Fowler's course). This is something that students have complained about in the forums, but thus far I've seen the staff stay firm (go them!).

Dr. Fowler takes a very different track towards his course. His course is a true intro-to-calculus course, and thus it has a different scope than Dr. Ghrist's course. But the differences between the two courses run much deeper than just the content. Dr. Fowler teaches so that the students understand the concepts. This means a few things: his course will take longer, first and foremost. There are 13 video lectures for the first week, and one would assume that there will be another 13 or so next week (there will be none next week for Dr. Ghrist - he works in two-week chunks). There will probably be over 100 video lectures in total (compared to my estimate of approximately 50 in Dr. Ghrist's class). Some of the video lectures are entirely aimed at giving evidence of an idea, like looking at how a ball bounces and calculating related limits and average velocities.

Thus far, the 'theory' has been about understanding limits and functions really well. To be fair, this level of understanding is assumed in Dr. Ghrist's class. But I have a hard time imagining that Dr. Fowler will suddenly top describing the why of each problem so much, or for Dr. Ghrist to start. It will be interesting to see if Dr. Fowler ever expects the students to be able to handle the theoretical aspects of calculus, as opposed to quizzing strictly computational techniques (which is all that he has tested so far).

I really hope that Dr. Fowler will emphasize some of the theory in the homeworks/quizzes, because I think he does a remarkable job. The lectures are not as polished as Dr. Ghrist's, and not everything is pre-rendered. Dr. Fowler has a tendency to actually write (lo and behold) on blackboards and what not. He also uses cutouts of TeXed formulas on wooden tables, or points his camera to him computer to show something. Some demonstrations are very clearly pre-fabricated, such as times when he integrates his writing with computer graphics (and uses a little silver knob to change the graphics when he needs). But throughout all of them, he comes across as a very enthusiastic and entertaining guy.

Dr. Fowler has extraordinary additional resources as well. He provides a free calculus textbook (it's boring, but free). And most importantly, he has an associated website that he refers to as mooculus, which seems great. It reminds me of the question and answer paradigm used by the Khan Academy. Immediate feedback that walks you through a series of progressively harder exercises on each subject. This is where much of the course prep time must have been spent, and it's great. In a sense, it babies students even more than Dr. Ghrist's class. But it also takes advantage of the open online format in a way that Dr. Ghrist's class does not.

The constant feedback from Dr. Fowler's mooculus seems to try to counter what I see as the largest problem facing an online calculus class - the lack of problem sessions or recitations. It's too early to tell so far how well this works - I've been helping some people on the forums with the same sort of questions that everyone asks. I think it's highly unfortunate that each of the calculus coursera classes usually has an inbuilt forum built on a stackexchange engine, but that won't ever actually be associated with math.stackexchange. There will be a lot of duplication, and there's a great amount of expertise on MSE that isn't present on coursera. On the flipside, there are many MSE users who have no problem essentially doing others' homework for them, so I understand the hesitation.

For people wanting to learn calculus for the first time, I would certainly recommend Dr. Fowler's first week at least. For people who need to have a strong mechanical understanding of Taylor Series expansions (which may include applied mathematicians or physicists), I think that Dr. Ghrist's class would serve that purpose. But the jury is still out on that one.

Leave a comment

Comment via email