In class today, we were asked to explain what was wrong with the following proof:
As $x$ increases, the function \begin{equation} f(x)=\frac{100x^2+x^2\sin(1/x)+50000}{100x^2} \end{equation} approaches (gets arbitrarily close to) 1.
Look at values of $f(x)$ as $x$ gets larger and larger. $$f(5) \approx 21.002$$ $$f(10)\approx 6.0010$$ $$f(25)\approx 1.8004$$ $$f(50)\approx 1.2002$$ $$f(100) \approx 1.0501$$ $$f(500) \approx 1.0020$$ These values are clearly getting closer to 1. QED
Of course, this is incorrect. Choosing a couple of numbers and thinking there might be a pattern does not constitute a proof.
But on a related note, these sorts of questions (where you observe a pattern and seek to prove it) can sometimes lead to strongly suspected conjectures, which may or may not be true. Here's an interesting one (with a good picture over at SpikedMath):
Draw $2$ points on the circumference of a circle, and connect them with a line. How many regions is the circle divided into? (two). Draw another point, and connect it to the previous points with a line. How many regions are there now? Draw another point, connecting to the previous points with lines. How many regions now? Do this once more. Do you see the pattern? You might even begin to formulate a belief as to why it's true.
But then draw one more point and its lines, and carefully count the number of regions formed in the circle. How many circles now? (It doesn't fit the obvious pattern).
So we know that the presented proof is incorrect. But lets say we want to know if the statement is true. How can we prove it? Further, we want to prove it without calculus - we are interested in an elementary proof. How should we proceed?
Firstly, we should say something about radians. Recall that at an angle $theta$ (in radians) on the unit circle, the arc-length subtended by the angle $theta$ is exactly $theta$ (in fact, this is the defining attribute of radians). And the value $sin theta$ is exactly the height, or rather the $y$ value, of the part of the unit circle at angle $theta$. It's annoying to phrase, so we look for clarification at the hastily drawn math below:
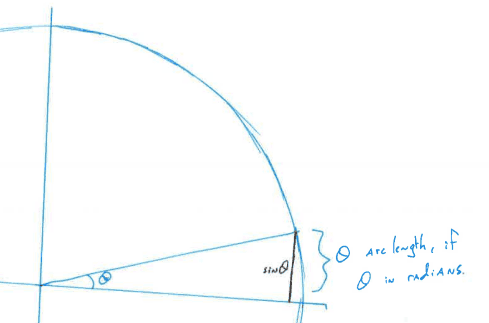
Note in particular that the arc length is longer than the value of $\sin \theta$, so that $\sin \theta < \theta$. (This relies critically on the fact that the angle is positive). Further, we see that this is always true for small, positive $\theta$. So it will be true that for large, positive $x$, we'll have $\sin \frac{1}{x} < \frac{1}{x}$. For those of you who know a bit more calculus, you might know that in fact, $\sin(\frac{1}{x}) = \frac{1}{x} - \frac{1}{x^33!} + O(\frac{1}{t^5})$, which is a more precise statement.
What do we do with this? Well, I say that this allow us to finish the proof.
$\dfrac{100x^2 + x^2 \sin(1/x) + 50000}{100x^2} leq \dfrac{100x^2 + x + 50000}{100x^2} = 1 + \dfrac{1}{100x} + \dfrac{50000}{100x^2}$
, and it is clear that the last two terms go to zero as $x$ increases. $\spadesuit$
Finally, I'd like to remind you about the class webpage. We don't use it often, but it is an avenue for extra information or to ask additional questions.
Info on how to comment
To make a comment, please send an email using the button below. Your email address won't be shared (unless you include it in the body of your comment). If you don't want your real name to be used next to your comment, please specify the name you would like to use. If you want your name to link to a particular url, include that as well.
bold, italics, and plain text are allowed in comments. A reasonable subset of markdown is supported, including lists, links, and fenced code blocks. In addition, math can be formatted using
$(inline math)$or$$(your display equation)$$.Please use plaintext email when commenting. See Plaintext Email and Comments on this site for more. Note also that comments are expected to be open, considerate, and respectful.