mixedmath

An Unfinished Example

At the end of class today, someone asked if we could do another example of a partial fractions integral involving an irreducible quadratic. We decided to look at the integral

$$ \int \frac{1}{(x^2 + 4)(x+1)}dx. $$ Notice that ${x^2 + 4}$ is an irreducible quadratic polynomial. So when setting up the partial fraction decomposition, we treat the ${x^2 + 4}$ term as a whole.

So we seek to find a decomposition of the form

$$ \frac{1}{(x^2 + 4)(x+1)} = \frac{A}{x+1} + \frac{Bx + C}{x^2 + 4}. $$ Now that we have the decomposition set up, we need to solve for ${A,B,}$ and ${C}$ using whatever methods we feel most comfortable with. Multiplying through by ${(x^2 + 4)(x+1)}$ leads to

$$ 1 = A(x^2 + 4) + (Bx + C)(x+1) = (A + B)x^2 + (B + C)x + (4A + C). $$ Matching up coefficients leads to the system of equations

$$\begin{align} 0 &= A + B \\ 0 &= B + C \\ 1 &= 4A + C. \end{align}$$ So we learn that ${A = -B = C}$, and ${A = 1/5}$. So ${B = -1/5}$ and ${C = 1/5}$.

Together, this means that

$$ \frac{1}{(x^2 + 4)(x+1)} = \frac{1}{5}\frac{1}{x+1} + \frac{1}{5} \frac{-x + 1}{x^2 + 4}. $$ Recall that if you wanted to, you could check this decomposition by finding a common denominator and checking through.

Now that we have performed the decomposition, we can return to the integral. We now have that

$$ \int \frac{1}{(x^2 + 4)(x+1)}dx = \underbrace{\int \frac{1}{5}\frac{1}{x+1}dx}_ {\text{first integral}} + \underbrace{\int \frac{1}{5} \frac{-x + 1}{x^2 + 4} dx.}_ {\text{second integral}} $$ We can handle both of the integrals on the right hand side.

The first integral is

$$ \frac{1}{5} \int \frac{1}{x+1} dx = \frac{1}{5} \ln (x+1) + C. $$

The second integral is a bit more complicated. It's good to see if there is a simple ${u}$-substition, since there is an ${x}$ in the numerator and an ${x^2}$ in the denominator. But unfortunately, this integral needs to be further broken into two pieces that we know how to handle separately.

$$ \frac{1}{5} \int \frac{-x + 1}{x^2 + 4} dx = \underbrace{\frac{-1}{5} \int \frac{x}{x^2 + 4}dx}_ {\text{first piece}} + \underbrace{\frac{1}{5} \int \frac{1}{x^2 + 4}dx.}_ {\text{second piece}} $$

The first piece is now a ${u}$-substitution problem with ${u = x^2 + 4}$. Then ${du = 2x dx}$, and so

$$ \frac{-1}{5} \int \frac{x}{x^2 + 4}dx = \frac{-1}{10} \int \frac{du}{u} = \frac{-1}{10} \ln u + C = \frac{-1}{10} \ln (x^2 + 4) + C. $$

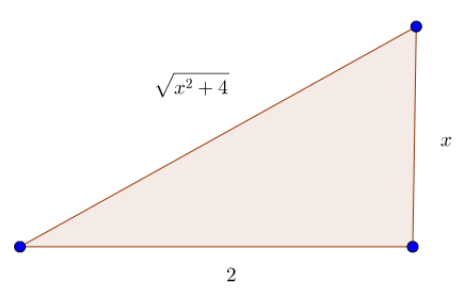
The second piece is one of the classic trig substitions. So we draw a triangle.

In this triangle, thinking of the bottom-left angle as ${\theta}$ (sorry, I forgot to label it), then we have that ${2\tan \theta = x}$ so that ${2 \sec^2 \theta d \theta = dx}$. We can express the so-called hard part of the triangle by ${2\sec \theta = \sqrt{x^2 + 4}}$.

Going back to our integral, we can think of ${x^2 + 4}$ as ${(\sqrt{x^2 + 4})^2}$ so that ${x^2 + 4 = (2 \sec \theta)^2 = 4 \sec^2 \theta}$. We can now write our integral as

$$ \frac{1}{5} \int \frac{1}{x^2 + 4}dx = \frac{1}{5} \int \frac{1}{4 \sec^2 \theta} 2 \sec^2 \theta d \theta = \frac{1}{5} \int \frac{1}{2} d\theta = \frac{1}{10} \theta. $$ As ${2 \tan \theta = x}$, we have that ${\theta = \text{arctan}(x/2)}$. Inserting this into our expression, we have

$$ \frac{1}{10} \int \frac{1}{x^2 + 4} dx = \frac{1}{10} \text{arctan}(x/2) + C. $$

Combining the first integral and the first and second parts of the second integral together (and combining all the constants ${C}$ into a single constant, which we also denote by ${C}$), we reach the final expression

$$ \int \frac{1}{(x^2 + 4)(x + 1)} dx = \frac{1}{5} \ln (x+1) - \frac{1}{10} \ln(x^2 + 4) + \frac{1}{10} \text{arctan}(x/2) + C. $$

And this is the answer.

Other Notes

If you have any questions or concerns, please let me know. As a reminder, I have office hours on Tuesday from 9:30–11:30 (or perhaps noon) in my office, and I highly recommend attending the Math Resource Center in the Kassar House from 8pm-10pm, offered Monday-Thursday. [Especially on Tuesday and Thursdays, when there tend to be fewer people there].

On my course page, I have linked to two additional resources. One is to Paul's Online Math notes for partial fraction decomposition (which I think is quite a good resource). The other is to the Khan Academy for some additional worked through examples on polynomial long division, in case you wanted to see more worked examples. This note can also be found on my website, or in pdf form.

Good luck, and I'll see you in class.

Leave a comment

Comment via email